状态自适应神经模糊推理系统S-ANFIS

状态自适应神经模糊推理系统(State-ANFIS，简称S-ANFIS)是 ANFIS 网络的简单推广，它通过区分状态变量和解释变量，为复杂系统建模提供了更灵活的框架。

S-ANFIS核心思想

S-ANFIS的关键创新在于它将输入变量分为两类：

• 状态变量(State Variables, $s$): 用于判断系统当前所处的宏观状态或工作模式
• 解释变量(Explanatory Variables, $x$): 在特定状态下解释或预测系统行为的变量

这种区分允许模型在不同状态下采用不同的参数配置，从而更好地适应复杂系统中的状态依赖行为模式。

S-ANFIS网络结构与数学表示

S-ANFIS采用两阶段神经模糊建模方法：

前提部分：状态判别与关联度计算

在前提部分，S-ANFIS只处理状态变量 $s$，目标是识别系统当前状态并计算与每个预定义状态的匹配程度。

假设有 $N_s$ 个状态变量，每个状态变量有 $M$ 个模糊隶属函数，则总共会有 $M^{N_s}$ 条模糊规则。前提参数总量为 $M^{N_s} \times K$，其中 $K$ 是每个隶属函数的可训练参数数量。

对于每个状态变量 $s_j$，模糊化后得到隶属度： \(\begin{equation} \mu_{j,m}(s_j) = \text{MF}_{j,m}(s_j; \theta_p) \end{equation}\)

其中 $\text{MF}_{j,m}$ 表示第 $j$ 个状态变量的第 $m$ 个隶属函数，$\theta_p$ 是前提参数集合。

规则触发强度通过T-范数(如乘积)计算： \(\begin{equation} w_i = \prod_{j=1}^{N_s} \mu_{j,m_j}(s_j) \end{equation}\)

其中 $i$ 是规则编号，$m_j$ 表示该规则对应的第 $j$ 个状态变量的隶属函数索引。

后果部分：解释变量加权与输出

在后果部分，S-ANFIS针对每个状态(规则)处理解释变量 $x$，建立对应的子模型。

对于第 $i$ 条规则，后果部分通常是解释变量的线性组合： \(\begin{equation} f_i(x) = p_{i0} + p_{i1}x_1 + p_{i2}x_2 + ... + p_{iN_x}x_{N_x} \end{equation}\)

其中 $p_{ij}$ 是需要优化的后果参数，$N_x$ 是解释变量的数量。后果参数总量为 $M^{N_s} \times (N_x+1)$。

最终输出：加权模型组合

S-ANFIS的最终输出是各规则输出的加权平均： \(\begin{equation} O = \frac{\sum_{i=1}^{M^{N_s}} w_i f_i(x)}{\sum_{i=1}^{M^{N_s}} w_i} \end{equation}\)

这种结构使得模型能够根据状态变量的值自适应地切换不同的子模型，实现更精确的预测。

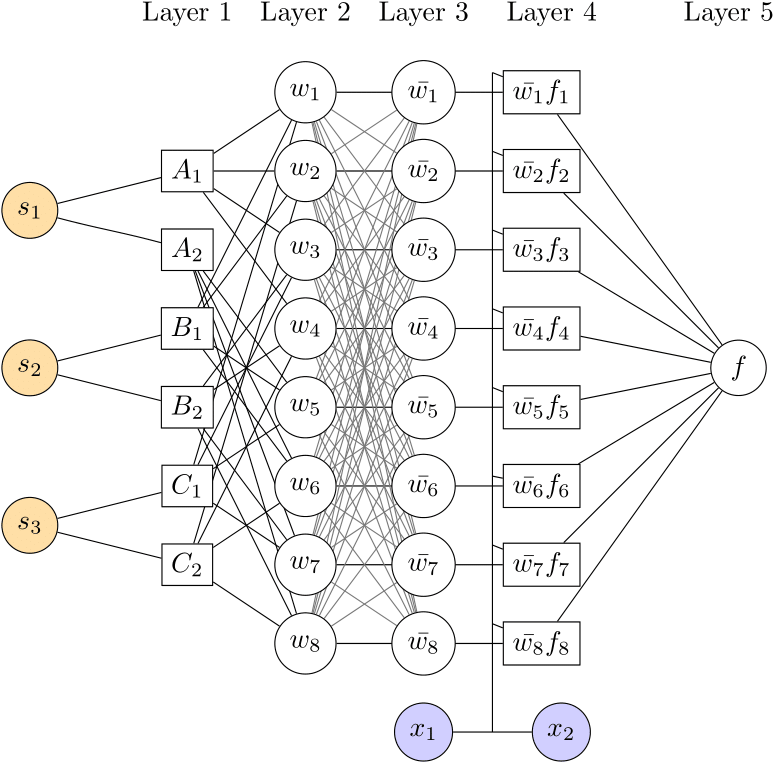
S-ANFIS网络示例

如上图所示，对于一个具有 $N_s=3$ 个状态变量和每个变量 $M=2$ 个隶属函数的S-ANFIS网络：

• 规则数量：$M^{N_s} = 2^3 = 8$ 条规则
• 前提参数量：$M^{N_s} \times K$，取决于隶属函数类型
• 后果参数量：$M^{N_s} \times (N_x+1) = 8 \times 3 = 24$，说明 $N_x = 2$，即有2个解释变量

这样的网络结构将输入空间划分为8个模糊子空间，每个子空间有各自的参数配置。

实现细节

初始化

S-ANFIS的实现中，前提参数通常在工作空间内等间隔初始化，以确保隶属函数有足够的重叠。目前支持三种隶属函数：

1. 广义钟形函数：\(\mu(x) = \frac{1}{1 + \left\lvert\frac{x-c}{a}\right\rvert^{2b}}\)
2. 高斯函数：$\mu(x) = e^{-\frac{(x-c)^2}{2\sigma^2}}$
3. S形函数：$\mu(x) = \frac{1}{1 + e^{-\gamma(x-c)}}$

后果参数则在 $[-0.5, 0.5]$ 范围内随机均匀初始化。

特征缩放

输入数据在拟合模型前进行标准化处理： \(\begin{equation} \tilde{x}_n = \frac{x_n - \mu_{x,train}}{\sigma_{x,train}} \quad \text{and} \quad \tilde{s}_n = \frac{s_n - \mu_{s,train}}{\sigma_{s,train}} \end{equation}\)

损失函数与优化

S-ANFIS采用均方误差(MSE)作为损失函数： \(\begin{equation} L(\theta) = MSE = \frac{1}{N}\sum_{n=1}^{N}(O_n - \tilde{y}_n)^2 \end{equation}\)

优化采用ADAM算法，并结合精英原则避免局部最优解：

数据被划分为训练样本和验证样本。\(\theta\)表示模型权重集合\(\theta^p\)（前提参数）和\(\theta^c\) （结果参数），这些权重采用不同的初始化方式。模型权重的更新基于训练损失函数 \(\operatorname{MSE}\left(O_{\text {train }}, \tilde{y}_{\text {train }}^b\right)\) ，其中 \(b\) 代表批次。为防止过拟合并实现正则化，系统采用早停机制：每当验证样本误差 \(L^{\prime}(\theta)\)改善时，当前模型参数\(\theta^*\)的副本将被保存。$p$用于记录样本外损失 \(L\left(O_{v a l}, y_{v a l}^b\right)\) 连续恶化的次数。耐心阈值 \(p_{\max }\) 规定了允许的最大连续恶化次数。当 \(p\) 达到 \(p_{\max }\) 时，系统会将当前模型权重与当前最优解进行比较，若新解在样本外损失方面更优则进行替换。此后所有优化参数和模型权重\(\theta\)将被重置，并在下一个训练周期重新开始迭代。参数更新次数取决于训练周期数和批次大小，因而影响计算资源——将批次大小减半会使模型权重更新次数翻倍。

S-ANFIS的优势与应用

S-ANFIS具有以下几个显著优势：

1. 状态感知建模：能够识别并适应系统的不同工作状态，为每种状态提供专门的子模型
2. 保留ANFIS优点：继承了ANFIS的专家知识转化能力、参数训练框架和可解释性
3. 灵活的模型架构：可以根据需要设置状态变量和解释变量，甚至可以允许它们重叠
4. 状态识别能力：前提部分本身可用于研究状态变量之间的动态交互，以及识别系统的不同工作模式

这种模型特别适用于具有多种工作状态或运行模式的复杂系统，如:

• 具有模式切换的工业控制系统
• 受外部因素影响的时间序列预测
• 非线性动力学系统建模

实现示例

S-ANFIS可通过PyTorch实现，以下是一个简单的使用示例：

import numpy as np
import torch
from sanfis import SANFIS, plottingtools
from sanfis.datagenerators import sanfis_generator

# 设置随机种子
np.random.seed(3)
torch.manual_seed(3)

# 生成数据
S, S_train, S_valid, X, X_train, X_valid, y, y_train, y_valid = sanfis_generator.gen_data_ts(
    n_obs=1000, test_size=0.33, plot_dgp=True)

# 定义隶属函数
membfuncs = [
    {'function': 'sigmoid',
     'n_memb': 2,
     'params': {'c': {'value': [0.0, 0.0],
                      'trainable': True},
                'gamma': {'value': [-2.5, 2.5],
                          'trainable': True}}},

    {'function': 'sigmoid',
     'n_memb': 2,
     'params': {'c': {'value': [0.0, 0.0],
                      'trainable': True},
                'gamma': {'value': [-2.5, 2.5],
                          'trainable': True}}}
]

# 创建模型
fis = SANFIS(membfuncs=membfuncs, n_input=2, scale='Std')
loss_function = torch.nn.MSELoss(reduction='mean')
optimizer = torch.optim.Adam(fis.parameters(), lr=0.005)

# 训练模型
history = fis.fit([S_train, X_train, y_train], [S_valid, X_valid, y_valid],
                  optimizer, loss_function, epochs=1000)

# 评估模型
y_pred = fis.predict([S, X])
plottingtools.plt_prediction(y, y_pred)

结论

S-ANFIS通过区分状态变量和解释变量，为复杂系统建模提供了一种灵活且强大的框架。它不仅可以适应系统的不同工作状态，还保留了传统ANFIS的优势，包括专家知识转化、参数训练和可解释性。这种模型在处理具有多种工作模式或状态依赖行为的系统时尤其有效。