Sobol 序列 — 准随机序列生成器及其 Python 实现

随机数在密码学、计算机图形学、统计学等众多领域都扮演着至关重要的角色。根据应用场景的不同，我们对随机数有不同的要求，从而也衍生出不同类型的随机数。Sobol 序列是一种特殊的序列，属于准随机数（Quasi-Random Numbers）的范畴，因其优异的均匀分布特性而在许多领域得到广泛应用。

引言：随机数的重要性与分类

在深入 Sobol 序列之前，我们先简单回顾一下随机数的几种主要类型：

• 统计学伪随机数 (Statistically Pseudorandom Numbers)： 指生成的随机数序列在统计特性上（如均匀性、独立性）近似于真正的随机序列。例如，对于一个伪随机比特流，0 和 1 的数量应大致相等。
• 密码学安全伪随机数 (Cryptographically Secure Pseudorandom Numbers, CSPRNG)： 除了满足统计学伪随机数的特性外，还要求从序列的一部分推断出其余部分在计算上是不可行的。这对于密钥生成等安全相关的应用至关重要。
• 真随机数 (True Random Numbers)： 其生成基于不可预测的物理过程（如热噪声、放射性衰变等），因此样本不可重现。获取真随机数的成本通常较高。

这些随机数的条件是逐渐增强的，获取难度也随之增加。因此，在实际应用中，我们需要根据具体需求选择合适的随机数生成方式。

准随机数生成器 (QRNG) 与低差异序列

在许多应用中，尤其是蒙特卡洛方法，我们需要的是能够在采样空间中均匀分布的点。准随机数生成器 (Quasi-Random Number Generator, QRNG) 就是为此目的设计的，它们生成的是所谓的低差异序列 (Low-Discrepancy Sequences)。

与伪随机数相比，低差异序列并非追求“看起来随机”，而是致力于更均匀、更系统地覆盖整个采样空间，避免点的高度聚集或大片空白区域。常见的低差异序列包括 Halton 序列、Faure 序列、Niederreiter 序列以及我们本文的主角——Sobol 序列。

所有基于现代 CPU 的随机数生成算法通常是伪随机的 (pseudorandom)，它们通过确定性算法生成序列，并在一个很长的周期后会重复。而准随机序列 (quasi-random)，如 Sobol 序列，也是确定性的，但其设计目标是低差异性，即高均匀度。

看待随机性的两个重要维度

从应用的角度来看，我们经常需要从两个维度来评价随机序列：

1. 统计随机性 (Statistical Randomness)： 序列在统计意义上的随机程度，如均匀性、相关性、重复周期等。这可以通过各种统计检验来评估。

2. 空间分布均匀性 (Spatial Uniformity)： 序列在空间中的分布特性，特别是在多维情况下。这通常可以用差异性 (Discrepancy) 来量化。

对于一个 $s$ 维单位超立方体 $[0,1]^s$ 中的点集 $P = {\mathbf{x}_1, \dots, \mathbf{x}_N}$，其差异性 $D_N(P)$ 可以表达为： \(\begin{equation} D_N(P) = \sup_{B \in J} \left| \frac{A(B; P)}{N} - \lambda_s(B) \right| \end{equation}\)

其中：

• $J$ 是 $[0,1]^s$ 中所有满足特定形状（如与坐标轴对齐的子矩形）的子区域的集合。
• $A(B; P)$ 是点集 $P$ 中落入子区域 $B$ 的点的数量。
• $N$ 是点集 $P$ 中点的总数量。
• $\lambda_s(B)$ 是子区域 $B$ 的 $s$ 维体积（或测度）。

简单来说，差异性衡量的是在最坏情况下，子区域内点的比例与该子区域体积之间的最大偏差。分布越均匀的点集，其差异性越低。

随着应用场景的不同，我们可能更关注其中一个维度。例如，在加密应用中，统计随机性更为重要；而在数值积分中，空间分布均匀性可能更为关键。准随机序列（如 Sobol 序列）正是在空间分布均匀性方面做了特别的优化。

什么是 Sobol 序列？

Sobol 序列是一系列 $n$ 维点，它们被设计成比标准伪随机序列更均匀地分布在单位超立方体 $[0, 1)^n$ 中。

• 确定性 (Deterministic)： 对于给定的维度和索引，Sobol 序列中的点是完全确定的，不像伪随机数那样依赖于随机种子（尽管某些实现允许”加扰”以引入随机性，同时保持低差异性）。
• 低差异性 (Low Discrepancy)： 这是 Sobol 序列的核心特性。差异性是衡量点集分布均匀性的一个指标。低差异意味着点集能够更好地避免出现大的空隙或过度聚集的区域。

下图直观地展示了伪随机点集与低差异序列点集的区别：

左边为伪随机数组成的二维点集，右边则是低差异序列（如 Sobol 序列）点集，对整个空间的覆盖更加完整和均匀。

Sobol 序列是如何生成的？

Sobol 序列的生成基于二进制算术和一组特殊的数字，称为方向数 (direction numbers) 或 初始化数 (initialization numbers)。其核心思想与 Radical Inversion 和 Van der Corput 序列 有关。

Radical Inversion 与 Van der Corput 序列

Radical Inversion 是一种将整数 $i$ 映射到 $[0,1)$ 区间的方法。对于一个基数 $b$，整数 $i$ 可以表示为 $b$ 进制数： \(\begin{equation} i = \sum_{l=0}^{M-1} a_l(i) b^l \end{equation}\)

其 Radical Inversion $\Phi_b(i)$（在 $C$ 为单位矩阵的简化情况下，即 Van der Corput 序列）定义为： \(\begin{equation} \Phi_b(i) = \sum_{l=0}^{M-1} a_l(i) b^{-l-1} \end{equation}\)

这相当于将 $i$ 的 $b$ 进制表示的小数点左边的数字镜像到小数点右边。

例如，以 2 为基的 Van der Corput 序列的前几项：

• $i=1=(1)_2 \implies \Phi_2(1) = (0.1)_2 = 1/2$
• $i=2=(10)_2 \implies \Phi_2(2) = (0.01)_2 = 1/4$
• $i=3=(11)_2 \implies \Phi_2(3) = (0.11)_2 = 3/4$
• $i=4=(100)_2 \implies \Phi_2(4) = (0.001)_2 = 1/8$

这个序列的每一个点都是取目前最长的未覆盖区域的中点，因此具有平均分布的特性。

Sobol 序列的构造

Sobol 序列的每一维都可以看作是一个以 2 为基，但使用了不同生成矩阵 $\mathbf{C}_j$（对应于方向数）的 Van der Corput 序列的推广。一个 $n$ 维 Sobol 序列的第 $i$ 个点 $\boldsymbol{X}_i$ 可以表示为： \(\begin{equation} \boldsymbol{X}_i = \left( \boldsymbol{\Phi}_{2, \mathbf{C}_1}(i), \boldsymbol{\Phi}_{2, \mathbf{C}_2}(i), \ldots, \boldsymbol{\Phi}_{2, \mathbf{C}_n}(i) \right) \end{equation}\)

其中 $\boldsymbol{\Phi}_{2, \mathbf{C}_j}(i)$ 是第 $j$ 维的坐标，通过对整数 $i$ 的二进制表示与第 $j$ 维的一组方向数（编码在 $\mathbf{C}_j$ 中）进行一系列位异或 (XOR) 操作得到。

具体来说，对于序列中的第 $k$ 个点和第 $j$ 维：

1. 将 $k$ 表示为二进制形式 $k = (b_m b_{m-1} \dots b_1)_2$。
2. 第 $j$ 维的坐标 $x_{k,j}$ 可以表示为 $x_{k,j} = b_1 v_{j,1} \oplus b_2 v_{j,2} \oplus \dots \oplus b_m v_{j,m}$，其中 $\oplus$ 是异或操作，$v_{j,r}$ 是第 $j$ 维对应的第 $r$ 个方向数（本身也是 $[0,1)$ 区间内的二进制小数）。

由于完全以 2 为底数，Sobol 序列的生成可以直接使用高效的位操作（如右移、异或）实现，计算速度非常快。选择合适的原始多项式和由此派生的方向数对于保证 Sobol 序列的低差异性至关重要。

一个显著的特性是，当样本数量 $N$ 为 $2$ 的整数次幂时（例如 $N=2^k$），Sobol 序列在 $[0,1)^s$ 区间中以 2 为底的每个基本区间 (elementary interval) 中都有且只会有一个点。这意味着它可以生成和分层采样 (Stratified Sampling) 或拉丁超立方采样 (Latin Hypercube Sampling) 同样高质量分布的样本，同时又不需要预先确定样本的总数量。

Sobol 采样的优缺点

优点：

1. 优越的均匀性： 特别是在高维空间，Sobol 序列能比伪随机数更有效地、更均匀地覆盖采样空间。
2. 更快的收敛速度： 在数值积分（准蒙特卡洛积分）中，对于 $s$ 维的积分问题，使用 $N$ 个点的标准蒙特卡洛方法的误差收敛速度通常是 $O(N^{-1/2})$。而使用低差异序列（如 Sobol 序列）的准蒙特卡洛方法，其误差收敛速度可以达到$O(N^{-1}(\log N)^s)$或更好。这意味着通常能用更少的样本点达到与 MC 方法相当的精度。
3. 确定性与可复现性： 由于序列是确定性生成的（不加扰时），结果是可复现的，这对于调试和比较非常有利。
4. 高效的参数空间探索： 适用于需要系统性探索多维参数空间的应用，如超参数优化、灵敏度分析等。
5. 逐点生成 (Progressive)： 可以逐点生成，不需要预先知道总样本数 $N$，并且已生成的序列是后续更长序列的前缀，保持了良好的分布特性。这非常适合渐进式采样。

缺点和注意事项：

1. 初始点的投影可能不佳： 对于较少的点数（例如，远小于 $2^d$，其中 $d$ 是维度），Sobol 序列在某些低维投影上可能表现出一定的规律性或对齐，看起来不够”随机”。
2. 方向数的质量： 序列的质量高度依赖于所使用的方向数。早期的一些方向数集在高维情况下表现可能不佳。现代实现通常使用经过优化的方向数集（例如，由 Joe 和 Kuo 提供的方向数）。
3. 维度限制： 虽然理论上 Sobol 序列可以扩展到非常高的维度，但高质量方向数的计算和存储会变得困难。对于极高维度（例如数千维），其相对于标准蒙特卡罗的优势可能会减弱或需要更复杂的加扰技术。通常，Sobol 序列在几十到几百维的问题中表现良好。
4. 加扰 (Scrambling)： 为了缓解初始点投影不佳的问题并改善有限样本下的随机性外观，可以对 Sobol 序列进行”加扰”（如随机线性加扰或数字移位）。加扰会引入一定的随机性，但旨在保持低差异特性。

Sobol 序列与规则网格采样 ( linspace) 的对比

一个常见的问题是：既然 Sobol 序列的目标是均匀分布，为什么不直接使用像 np.linspace 这样的函数在每个维度上创建等距点，然后组合它们形成一个规则的多维网格呢？

虽然规则网格在低维（如1D或2D）下直观且易于实现均匀覆盖，但在多维空间和许多实际应用场景中，Sobol 序列等低差异序列通常更具优势。主要原因如下：

1. 维度灾难 (Curse of Dimensionality)：
   • 规则网格： 若在 $d$ 维空间中，每个维度取 $k$ 个点，总点数将是 $k^d$。随着维度 $d$ 的增加，所需点数会呈指数级增长，迅速变得计算上不可行。例如，10 个维度各取 10 个点就需要 $10^{10}$ （一百亿）个样本。
   • Sobol 序列： 可以灵活地生成任意数量 $N$ 的样本点，这些点共同致力于均匀填充 $d$ 维空间，而 $N$ 通常远小于 $k^d$，使其在高维情况下更为实用。
2. 投影特性与”对齐”伪影：
   • 规则网格： 点严格排列在网格线上，形成高度规则的结构。这种规律性可能导致采样点与被研究函数或现象的特定结构对齐，从而产生系统性偏差。
   • Sobol 序列： 虽然也是确定性的，但其设计旨在最小化”差异性”，使得点在各种子区域（尤其是轴对齐的）中分布更均匀，避免了网格的僵硬结构，并力求在低维投影上也展现良好的分布。
3. 逐点生成 (Progressive Property)：
   • 规则网格： 通常需要预先确定总点数和网格结构。若需增加样本，往往要重新生成整个更密的网格，原有样本可能无法直接复用。
   • Sobol 序列： 具有逐点生成的特性。可以先生成 $N_1$ 个点，如果需要更高精度，可以继续生成额外的点，形成一个包含 $N_1+N_2$ 个点的序列，该序列的前 $N_1$ 个点与原序列一致，且整个序列仍保持低差异性。这对于渐进式改进和自适应采样非常有利。
4. 积分收敛性与效率：
   • 规则网格 (用于数值积分)： 虽然某些基于网格的求积法则（如梯形或辛普森法则）对光滑函数有较好的收敛阶，但它们受限于固定的网格结构，且在高维下常数因子可能很差。
   • Sobol 序列 (用于准蒙特卡罗积分, QMC)： QMC 方法的误差收敛速度理论上可达 $O(N^{-1}(\log N)^s)$，通常优于标准蒙特卡罗的 $O(N^{-1/2})$。对于中高维度，QMC 通常比依赖固定网格的确定性求积规则更灵活且高效。
5. 空间”填充”方式：
   • 规则网格： 像是在空间中规则地铺设”瓷砖”。
   • Sobol 序列： 更像是在空间中”智能地”布置点，以确保覆盖全面且避免空隙和聚集，同时不像网格那样死板。

linspace 生成的规则网格主要保证了单维度上的等距性，而 Sobol 序列则致力于实现整个多维空间的低差异性和高均匀度。因此，在高维问题、需要逐点生成能力、或追求更快积分收敛速度的应用中，Sobol 序列是比规则网格采样更优越的选择。规则网格采样更适用于维度非常低、或需要严格控制各维度采样位置的简单场景。

Sobol 采样的主要应用领域

Sobol 采样因其优越的特性被广泛应用于多个领域：

1. 数值积分 (Numerical Integration)： 这是 Sobol 序列最经典和最主要的应用，即准蒙特卡洛积分。
2. 金融工程 (Financial Engineering)： 用于衍生品定价（如期权定价）、风险价值 (VaR) 计算、信用风险模型等。
3. 计算机图形学 (Computer Graphics)： 用于全局光照算法（如路径追踪、光线追踪中的采样）、抗锯齿等，以产生更平滑、更真实的图像。
4. 灵敏度分析 (Sensitivity Analysis)： 评估模型输出对输入参数变化的敏感程度，Sobol 采样可以有效地探索参数空间。
5. 优化 (Optimization)： 作为某些全局优化算法（如基于粒子群的算法或模拟退火）的初始化或搜索策略。
6. 物理和工程模拟： 在需要进行大量模拟和参数研究的领域。
7. 机器学习： 例如在超参数优化中探索参数组合，以期更有效地找到最优配置。

Python 中的 Sobol 序列实现

Python 中有多个库提供了 Sobol 序列的实现，其中最常用的是 SciPy 和 PyTorch。

使用 SciPy (scipy.stats.qmc.Sobol)

SciPy 的 stats.qmc (Quasi-Monte Carlo) 模块提供了 Sobol 类。

# 1. 初始化 Sobol 序列生成器
dimension = 2  # 定义维度
# Sobol 序列生成器，可以指定 scramble=True 进行加扰
sobol_engine = qmc.Sobol(d=dimension, scramble=False, seed=None) # seed 用于加扰时的随机性

# 2. 生成样本点
num_samples = 128
samples = sobol_engine.random(n=num_samples) # 生成 num_samples 个点

print(f"Generated {num_samples} Sobol samples of dimension {dimension}:")
print(samples[:5]) # 打印前5个样本点

# 3. 跳过初始点 (可选)
# 有时为了更好的分布特性，会跳过序列的初始部分
# sobol_engine_skipped = qmc.Sobol(d=dimension, scramble=False)
# sobol_engine_skipped.fast_forward(1024) # 跳过前1024个点
# samples_skipped = sobol_engine_skipped.random(n=num_samples)
# print("\nSobol samples after skipping 1024 points:")
# print(samples_skipped[:5])

# 4. 使用加扰 (Scrambling)
sobol_engine_scrambled = qmc.Sobol(d=dimension, scramble=True, seed=42)
samples_scrambled = sobol_engine_scrambled.random(n=num_samples)
print("\nScrambled Sobol samples:")
print(samples_scrambled[:5])
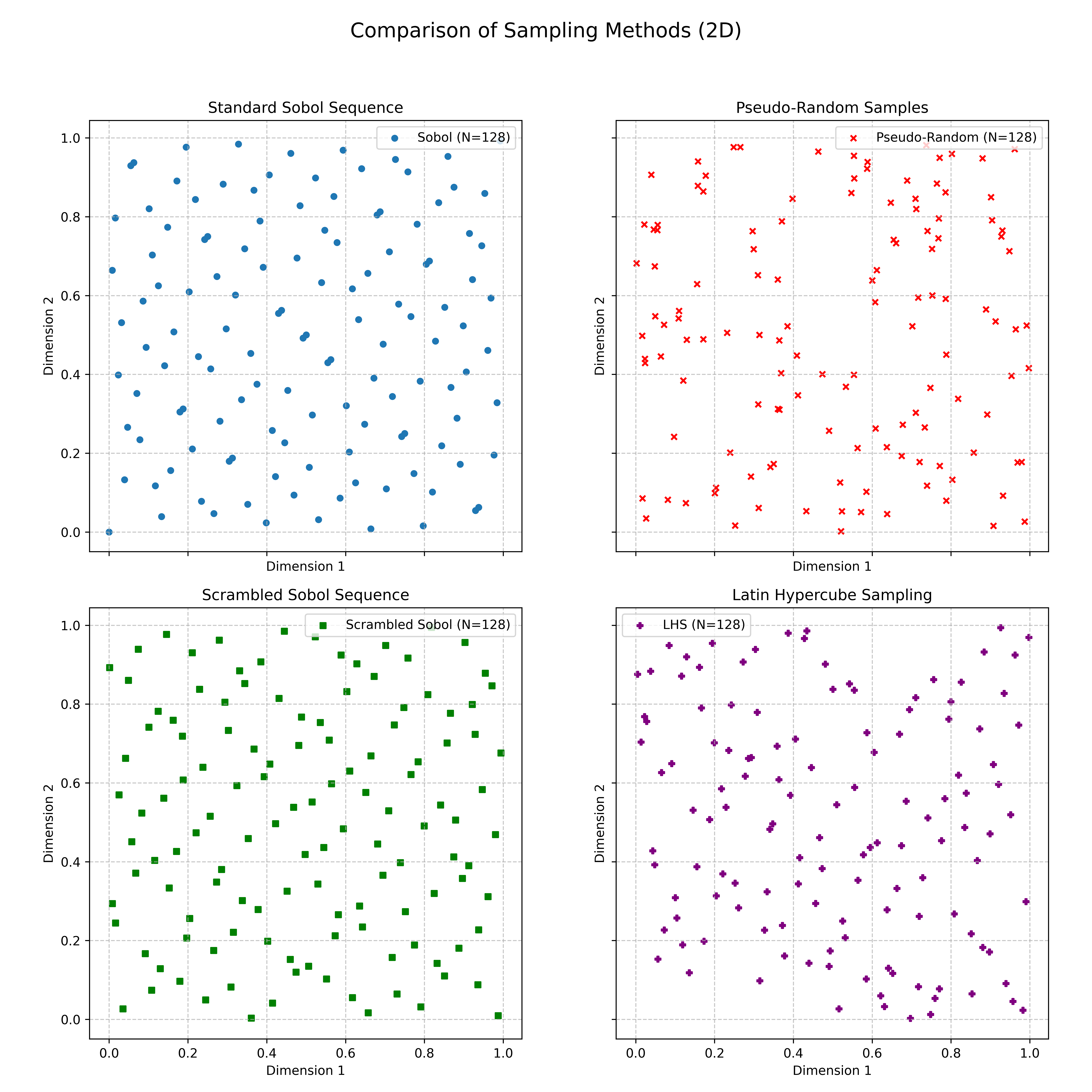
if dimension == 2:
    fig, axs = plt.subplots(2, 2, figsize=(12, 12), sharex=True, sharey=True)  # 调整为2x2布局

    # 普通 Sobol 序列
    axs[0, 0].scatter(samples[:, 0], samples[:, 1], s=20, marker='o', label=f'Sobol (N={num_samples})')
    axs[0, 0].set_title('Standard Sobol Sequence')
    axs[0, 0].set_xlabel('Dimension 1')
    axs[0, 0].set_ylabel('Dimension 2')
    axs[0, 0].set_aspect('equal', adjustable='box')
    axs[0, 0].legend()
    axs[0, 0].grid(True, linestyle='--', alpha=0.7)

    # 伪随机数作为对比
    pseudo_random_samples = np.random.rand(num_samples, dimension)
    axs[0, 1].scatter(pseudo_random_samples[:, 0], pseudo_random_samples[:, 1], s=20, marker='x', color='red',
                      label=f'Pseudo-Random (N={num_samples})')
    axs[0, 1].set_title('Pseudo-Random Samples')
    axs[0, 1].set_xlabel('Dimension 1')
    axs[0, 1].set_ylabel('Dimension 2')
    axs[0, 1].set_aspect('equal', adjustable='box')
    axs[0, 1].legend()
    axs[0, 1].grid(True, linestyle='--', alpha=0.7)

    # 加扰的 Sobol 序列
    axs[1, 0].scatter(samples_scrambled[:, 0], samples_scrambled[:, 1], s=20, marker='s', color='green',
                      label=f'Scrambled Sobol (N={num_samples})')
    axs[1, 0].set_title('Scrambled Sobol Sequence')
    axs[1, 0].set_xlabel('Dimension 1')
    axs[1, 0].set_ylabel('Dimension 2')
    axs[1, 0].set_aspect('equal', adjustable='box')
    axs[1, 0].legend()
    axs[1, 0].grid(True, linestyle='--', alpha=0.7)

    # 拉丁超立方采样 (LHS)
    lhs_engine = qmc.LatinHypercube(d=dimension, seed=42)
    samples_lhs = lhs_engine.random(n=num_samples)
    axs[1, 1].scatter(samples_lhs[:, 0], samples_lhs[:, 1], s=20, marker='P', color='purple',
                      label=f'LHS (N={num_samples})')
    axs[1, 1].set_title('Latin Hypercube Sampling')
    axs[1, 1].set_xlabel('Dimension 1')
    axs[1, 1].set_ylabel('Dimension 2')
    axs[1, 1].set_aspect('equal', adjustable='box')
    axs[1, 1].legend()
    axs[1, 1].grid(True, linestyle='--', alpha=0.7)

    plt.suptitle('Comparison of Sampling Methods (2D)', fontsize=16)
    plt.tight_layout(rect=[0, 0, 1, 0.95])  # 调整布局适应标题
    plt.savefig('sampling_methods_2d.png', dpi=600)
    plt.show()

说明：

• qmc.Sobol(d=dimension, scramble=False): 初始化一个 Sobol 序列生成器。d 是维度。scramble=True 会启用加扰，这通常能改善有限样本的质量，但会失去纯粹的确定性（加扰本身是随机的，但对于固定的种子，加扰后的序列是确定的）。
• sobol_engine.random(n=num_samples): 生成 num_samples 个样本点。每个点是一个 dimension 维的向量，其分量在 $[0, 1)$区间内。
• sobol_engine.fast_forward(m): 可以跳过序列中的前 m 个点。
• seed: 当 scramble=True 时，seed 控制加扰的随机性，以确保可复现性。

使用 PyTorch (torch.quasirandom.SobolEngine)

PyTorch 也提供了 SobolEngine 用于生成 Sobol 序列，这对于在 PyTorch 生态系统中进行工作（例如，在深度学习模型的超参数搜索或基于梯度的期望估计中）非常方便。

import torch
from torch.quasirandom import SobolEngine

# 1. 初始化 SobolEngine
dimension = 2
# scramble=True 进行加扰, seed 用于复现加扰结果
sobol_engine_torch = SobolEngine(dimension=dimension, scramble=False, seed=None)

# 2. 生成样本点
num_samples = 128
# draw 方法返回一个 Tensor
samples_torch = sobol_engine_torch.draw(num_samples) 

print(f"\nGenerated {num_samples} Sobol samples using PyTorch (dimension {dimension}):")
print(samples_torch[:5])

# 3. 使用加扰
sobol_engine_torch_scrambled = SobolEngine(dimension=dimension, scramble=True, seed=42)
samples_torch_scrambled = sobol_engine_torch_scrambled.draw(num_samples)
print("\nScrambled Sobol samples using PyTorch:")
print(samples_torch_scrambled[:5])

说明：

• SobolEngine(dimension=dimension, scramble=False, seed=None): 初始化引擎。dimension 是维度。scramble=True 启用加扰。seed 用于在加扰时固定随机数生成器状态。
• sobol_engine_torch.draw(num_samples): 生成 num_samples 个样本点，返回一个 PyTorch Tensor。
• PyTorch 的 SobolEngine 最高支持约 1111 维（截至较新版本，具体请查阅官方文档），并且其方向数是经过优化的。

不同采样方法的比较

为了更好地理解 Sobol 序列的特性，下表总结了它与其他几种常见采样方法的对比：

特性	伪随机数 (PRNG)	网格采样 (Grid Sampling)	拉丁超立方采样 (LHS)	Halton/Hammersley 序列	Sobol 序列
类型	伪随机 (Pseudo-Random)	确定性 / 系统性 (Deterministic/Systematic)	分层随机 (Stratified Random)	准随机 (Quasi-Random)	准随机 (Quasi-Random)
均匀性/覆盖度	可能出现聚集和空隙	规则，但可能在高维下效率低；易产生规律性伪影	确保每个一维投影上的分层均匀	良好，但低维投影可能不如 Sobol	非常好，尤其在高维下
差异性	较高	较低（但结构固定）	中等至较低	低	非常低
收敛速度 (积分)	$O(N^{-1/2})$	取决于函数，可能较差	通常优于 PRNG，接近 $O(N^{-1})$ (视情况)	$O(N^{-1}(\log N)^s)$ 或更好	$O(N^{-1}(\log N)^s)$ 或更好
确定性	否 (依赖种子)	是	否 (分层内随机)	是	是 (不加扰时)
逐点生成	是	通常否 (需预定总点数和网格结构)	通常否 (需预定总点数)	是	是
计算成本 (生成)	非常低	低	低至中等	低	低 (基于位操作)
相关性/模式	低（理论上），但周期有限	强烈的规律性，轴对齐模式	避免一维投影的聚集，但高维投影可能仍有结构	某些基数选择下初始点可能线性相关	初始点投影可能不佳 (可通过加扰改善)
主要优点	实现简单，速度快	简单直观	保证一维投影的良好覆盖，对某些模型有效	良好的均匀性，确定性	极佳的均匀性，快速收敛，逐点生成
主要缺点	收敛慢，高维下覆盖不均	“维度灾难”，高维下点数剧增，不灵活	高维下均匀性可能不如 QMC，非逐点	初始点问题，某些基数选择敏感	初始点问题，方向数质量依赖
典型用例	通用随机模拟，游戏，密码学 (CSPRNG)	低维参数扫描，可视化	计算机实验设计，不确定性量化，优化	数值积分，参数空间探索	数值积分，金融，图形学，灵敏度分析
Python 示例	numpy.random.rand() torch.rand()	numpy.meshgrid() itertools.product()	scipy.stats.qmc.LatinHypercube	scipy.stats.qmc.Halton	scipy.stats.qmc.Sobol torch.quasirandom.SobolEngine

一些解释：

• 网格采样 (Grid Sampling): 指的是在每个维度上取等间隔的点，然后组合它们。虽然在低维下直观，但在高维下所需的点数会爆炸式增长（维度灾难）。
• 分层采样 (Stratified Sampling): 思想是将空间划分为若干不重叠的子区域（层），然后在每个子区域内独立采样。LHS 是分层采样的一种特殊形式。
• 拉丁超立方采样 (LHS): 将每个维度划分为 $N$ 个等概率的区间，然后从每个区间中随机抽取一个值，确保在每个维度的每个分层中都有一个样本点，并将这些值随机组合。它保证了一维投影的均匀性。
• Halton/Hammersley 序列: 也是经典的低差异序列，Halton 基于不同素数为基的 Van der Corput 序列，Hammersley 则在其基础上修改第一维。

Sobol 序列通常被认为是综合性能最好的低差异序列之一，尤其是在需要高维均匀采样和快速收敛的准蒙特卡罗积分中。

总结

Sobol 序列作为一种经典的低差异序列，通过其确定性的生成方式和优异的均匀分布特性，在多维空间采样方面表现出色。它能够比传统的伪随机数更有效地填充采样空间，从而在数值积分、金融建模、计算机图形学以及机器学习等多个领域中提高计算效率和结果精度。

尽管存在一些如初始点分布和维度限制等问题，但通过现代实现中使用的优化方向数和加扰技术，Sobol 序列仍然是科学计算和工程实践中一个强大且有价值的工具。Python 中的 SciPy 和 PyTorch 等库使得 Sobol 序列的获取和使用变得非常便捷。