多目标优化的性能度量

在多目标优化中，由于解通常不是单一的，而是一个帕累托最优解集（或其近似），我们需要合适的性能度量指标来评估算法找到的解集的质量。这些指标主要关注两个方面：

1. 收敛性 (Convergence): 找到的解尽可能接近真实的帕累托前沿。
2. 多样性 (Diversity/Spread): 找到的解在帕累托前沿上分布尽可能广泛和均匀，以代表各种不同的权衡方案。

超体积HV及其变体

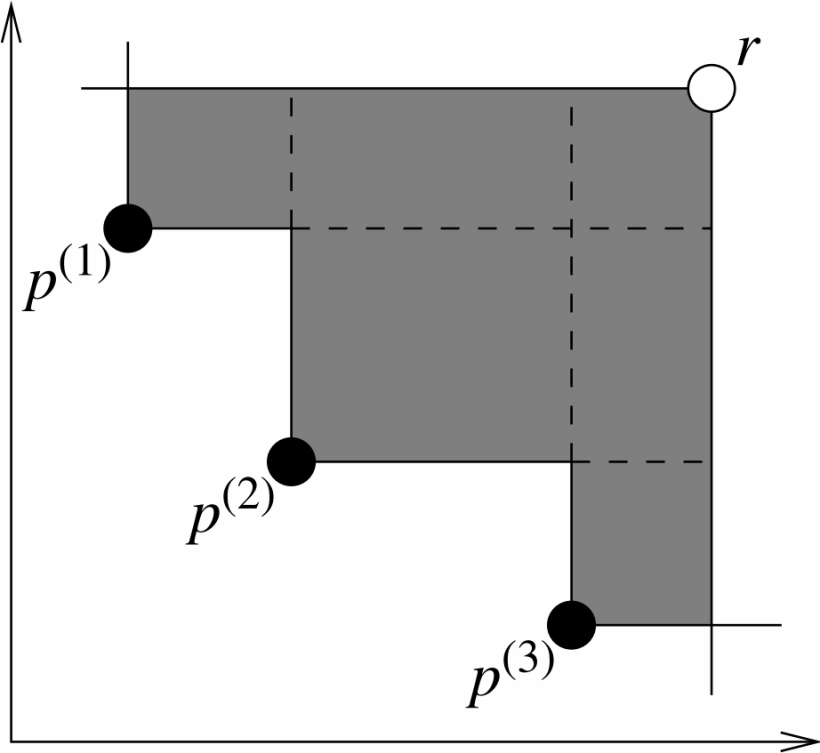
超体积（Hypervolume，HV）：

![Desktop View] 两目标问题的超体积指标

定义：超体积指标衡量的是由解集中的点与一个预定义的参考点（Reference Point）在目标空间中所围成的区域的“体积”（或面积，如果是二维）。参考点通常选择一个在所有目标维度上都比解集中任何解都“差”的点（例如，对于最小化问题，参考点的每个分量都大于解集中对应目标分量的最大值）。HV值越大，通常表示解集的综合性能越好，因为它意味着解集更接近真实的帕累托前沿并且/或者具有更好的分布。

计算步骤：

• 确定参考点(Reference Point)：参考点通常是一个在所有目标上都比解集中的所有解要差的点。例如，对于一个最小化问题，参考点的每个坐标可以是目标值中的最大值再加上一个较大的偏移量。对于 $k$ 个最小化的目标，参考点 $R=(r_1,r_2,…,r_k)$ 应满足对于解集 $S$ 中的任意解 $s=(s_1,…,s_k)$，都有 $s_i<r_i$对所有 $i=1,…,k$成立（严格来说，对于计算，通常是 $s_i\leq r_i$）。
• 计算贡献体积：对于解集 $S $中的每个非支配解，计算其与参考点构成的超矩形区域，并排除被其他解支配的部分。
• 加总不重叠体积：将所有非支配解贡献的不重叠超矩形体积加起来得到总的超体积。

\[\begin{equation} H V(\mathcal{S})=\text { Volume }\left(\bigcup_{\mathbf{s} \in \mathcal{S}}\{\mathbf{x} \mid \mathbf{s} \preceq \mathbf{x} \preceq \mathbf{R}\}\right) \end{equation}\]

更严谨的定义是基于勒贝格测度： \(\begin{equation} H V(\mathcal{S}, \mathbf{R})=\lambda\left(\bigcup_{\mathbf{s} \in \mathcal{S}} ⟦𝐬, 𝐑⟧\right) \end{equation}\) 其中 ⟦𝐬, 𝐑⟧表示由 s 和 R 界定的超矩形，$\lambda$是勒贝格测度。

优点：

1. 严格帕累托遵从性：如果解集$A$帕累 托支配解集$B$，则$HV(A)≥HV(B)$。
2. 能够同时衡量收敛性和多样性。
3. 不需要真实的帕累托前沿信息。

缺点：

1. 计算复杂度高，尤其在高维目标空间（通常 $k>3$ 时计算非常耗时）。
2. 对参考点的选择敏感。
3. 对目标的尺度敏感，通常需要先对目标值进行归一化。

代码实现：

   def calculate_hv_2d_min(solution_set, reference_point):
       """
       计算2D最小化问题的超体积。
       solution_set: (n_solutions, 2) array, 每一行是一个解的目标值。
       reference_point: (2,) array, 参考点。
       """
       # 确保解集是numpy数组
       solutions = np.array(solution_set)
       ref_point = np.array(reference_point)
   
       # 过滤掉被参考点支配的解 (或者目标值大于等于参考点的解)
       # 这里假设所有解都优于参考点
       valid_solutions = []
       for s in solutions:
           if np.all(s < ref_point): # 对于最小化问题
               valid_solutions.append(s)
       if not valid_solutions:
           return 0.0
       
       solutions = np.array(valid_solutions)
   
       # 按照第一个目标值从小到大排序
       # 如果第一个目标值相同，则按第二个目标值从小到大排序 (有助于处理)
       sorted_indices = np.lexsort((solutions[:, 1], solutions[:, 0]))
       sorted_solutions = solutions[sorted_indices]
   
       hv = 0.0
       # 对于最小化问题，我们从 "最差" 的y值（即参考点的y值）开始
       previous_y = ref_point[1] 
   
       for i in range(sorted_solutions.shape[0]):
           # 当前解的x值与参考点x值的差作为宽度
           width = ref_point[0] - sorted_solutions[i, 0]
           # 高度是上一个有效解的y值（或初始参考y值）与当前解y值的差
           height = previous_y - sorted_solutions[i, 1]
           
           if width > 0 and height > 0: # 只有当形成有效矩形时才增加体积
               hv += width * height
           
           # 更新previous_y为当前解的y值，因为下一个矩形不能覆盖到当前解的y值以下
           previous_y = sorted_solutions[i, 1] 
           
           # 如果当前解的x值已经超出参考点，后续解不可能贡献HV
           if sorted_solutions[i,0] >= ref_point[0]:
               break
       return hv
   
   # 示例
   # solutions = np.array([[1, 5], [2, 3], [3, 4], [4, 1]])
   # ref_point = np.array([6, 7])
   # hv_value = calculate_hv_2d_min(solutions, ref_point)
   # print(f"Hypervolume (2D Min): {hv_value}")

Pymoo调用：

from pymoo.indicators.hv import HV
import numpy as np

# 假设 F 是一个 (n_solutions, n_objectives) 的Numpy数组，包含解集的目标值
# F = np.array([[1, 5], [2, 3], [3, 4], [4, 1]]) # 示例解集 (最小化)

# 假设 ref_point 是参考点 (对于最小化问题，应大于所有解的目标值)
# ref_point = np.array([6.0, 7.0])

# 初始化HV指标计算器
# Pymoo的HV默认处理最小化问题
# ind = HV(ref_point=ref_point)

# 计算HV值
# hv_value = ind(F)
# print(f"Hypervolume (Pymoo): {hv_value}")

平均超体积MHV：

MHV指多目标优化算法在多次独立运行后得到的超体积（HV）值的平均值，用于评估算法的稳定性和平均性能。 \(\begin{equation} M H V=\frac{1}{N_{\text {runs }}} \sum_{i=1}^{N_{\text {runs }}} H V_i \end{equation}\)

​ 其中$N_{runs}$是算法的运行次数，$HV_i$是第 $i$次运行得到的解集的超体积。where $N_{runs}$ is the number of runs, and $HV_i$ is the hypervolume of the solution set from the i-th run.

​ 优点为能反映算法的平均性能，减少单次运行的随机性带来的影响。缺点是需要多次运行算法，计算成本较高。

超体积差HVD：

HVD通常指真实的帕累托前沿（如果已知）的超体积与算法找到的解集的超体积之间的差值。 \(\begin{equation} H V D=H V\left(P F_{\text {true }}\right)-H V\left(P F_{\text {approx }}\right) \end{equation}\) 其中$PF_{\text {true }}$是真实的帕累托前沿，$PF_{\text {approx}}$ 是算法找到的近似帕累托前沿。$HVD$越小越好。如果$PF_{\text {true }}$未知，有时会用一个高质量的参考前沿代替。 另一种形式是相对超体积差，或称为超体积比率的不足部分：$1-H V\left(P F_{\text {approx }}\right) / H V\left(P F_{\text {true }}\right)$。

世代距离GD及其变种

世代距离GD（Generational Distance）：

GD衡量算法找到的近似帕累托前沿$PF_{\text {approx}}$中的每个解到真实帕累托前沿 $PF_{\text {true }}$的平均最小距离。它主要评估解集的收敛性。GD值越小，表示解集越接近真实的帕累托前沿。

计算步骤：

• 确定真实的帕累托前沿$PF_{\text {true }}$：这是一组已知的最优解。
• 确定计算解集$PF_{\text {approx}}$：这是算法找到的解集。
• 计算每个解与真实帕累托前沿之间的最小欧氏距离：对于$PF_{\text {approx}}$中的每个解，计算它与 $PF_{\text {true }}$上所有解$z_j$的欧氏距离，并取最小值 $d_i = \min_{z_j \in PF_{\text{true}}} \operatorname{distance}\left(x_i, z_j\right)$。
• 计算所有解的距离的平均值：

\[\begin{equation} G D_p\left(P F_{\text {approx }}, P F_{\text {true }}\right)=\left(\frac{1}{\left|P F_{\text {approx }}\right|} \sum_{i=1}^{\left|P F_{\text {approx }}\right|} d_i^p\right)^{1 / p} \end{equation}\]

通常 $p=2$（欧氏距离的均方根），简化为： \(GD = \frac{1}{|PF_{approx}|} \sum_{i=1}^{|PF_{approx}|} \min_{\mathbf{z} \in PF_{true}} \sqrt{\sum_{k=1}^M (f_k(\mathbf{x}_i) - f_k(\mathbf{z}))^2}\) 其中 $M$ 是目标数，$f_k(\mathbf{x}_i)$ 和 $f_k(\mathbf{z})$ 分别是解 $\mathbf{x}_i$ 和 $\mathbf{z}$ 在第 $k$ 个目标上的值。

优点：

1. 直观，易于理解和计算。
2. 能有效衡量解集的收敛性。

缺点：

1. 需要真实的帕累托前沿，这在许多实际问题中是未知的。
2. 如果近似解集只有少数几个点且都非常接近真实前沿的某个小区域，GD值可能很小，但这并不能反映解集的多样性。
3. 对$PF_{\text {true }}$中点的数量和分布敏感。

代码实现：

def calculate_gd(solution_set, reference_set):
    """
    计算世代距离 GD。
    solution_set: (n_solutions, n_objectives) array, 算法找到的解集。
    reference_set: (n_ref_points, n_objectives) array, 真实的帕累托前沿。
    """
    solution_set = np.array(solution_set)
    reference_set = np.array(reference_set)
    
    sum_min_distances_sq = 0.0
    for sol_point in solution_set:
        # 计算当前解到所有真实前沿点的欧氏距离的平方
        distances_sq = np.sum((reference_set - sol_point)**2, axis=1)
        min_distance_sq = np.min(distances_sq)
        sum_min_distances_sq += min_distance_sq # 或者直接加min_distance，然后最后除以N再开方

    # GD 通常是距离的均值或均方根，这里用均方根的平方，然后开方
    # 或者直接用距离的均值 (p=1)
    # gd_value = np.sqrt(sum_min_distances_sq / solution_set.shape[0]) # p=2
    
    # 更常见的GD是直接平均最小距离 (p=1 in the sum, then average)
    # Pymoo的GD是 (sum d_i^p / N)^(1/p)
    # 如果p=1，则 (sum d_i / N)
    # 如果p=2，则 (sum d_i^2 / N)^(1/2)

    # 为与Pymoo的GD(p=1)定义一致:
    accum_dist = 0
    for s_point in solution_set:
        dist = np.min(np.sqrt(np.sum((reference_set - s_point)**2, axis=1)))
        accum_dist += dist
    gd_value = accum_dist / solution_set.shape[0]
    return gd_value

# solutions = np.array([[1.1, 4.9], [2.2, 2.8]])
# pf_true = np.array([[1, 5], [2, 3], [3,4], [4,1]])
# gd_val = calculate_gd(solutions, pf_true)
# print(f"GD: {gd_val}")

Pymoo调用实现：

from pymoo.indicators.gd import GD
import numpy as np

# F = np.array([[1.1, 4.9], [2.2, 2.8]]) # 算法找到的解集
# pf_true = np.array([[1, 5], [2, 3], [3,4], [4,1]]) # 真实帕累托前沿

# 初始化 GD 指标计算器，pf_true 是真实前沿
# ind = GD(pf_true, norm=False) # norm=False 使用欧氏距离, Pymoo的GD默认p=1
                             # Pymoo的GD.py定义为 (1/n * sum(d_i^p))^(1/p)
                             # d_i = min_{z in PF_true} ||f(x_i) - f(z)||_p_dist
                             # 默认 p_dist = 2 (欧氏距离), p = 1 (用于聚合)

# 计算 GD 值
# gd_value = ind(F)
# print(f"GD (Pymoo): {gd_value}")

GD+

GD+ (Generational Distance Plus) 是GD的一个变体，它在计算距离时考虑了支配关系。对于 $PF_{\text {approx}}$中的一个解 $x$，如果它被 $PF_{\text {true }}$中的某个解 $z $支配，那么它们之间的距离就是从 $x$移动到 $z $所需的“修正距离”（通常是各目标分量差值之和，只考虑 $x$比 $z $差的部分）。如果 $x$不被 $PF_{\text {true }}$中的任何解支配（即 $x$位于真实前沿之上或之外），则其距离为0。GD+值越小越好。

\(\begin{equation} d^{+}\left(x, P F_{\text {true }}\right)= \begin{cases}\sqrt{\sum_{k=1}^M\left(\max \left\{0, f_k(x)-f_k\left(z_x^*\right)\right\}\right)^2} & \text { if } x \text { is dominated by some } z \in P F_{\text {true }} \\ 0 & \text { otherwise }\end{cases} \end{equation}\) 其中 $z_x^*$ 是 $P F_{\text {true }}$ 中“最接近地支配”$x$ 的点（或一个能支配 $x$ 的参考点）。更准确地说，它是基于“支配距离惩罚”。 \(\begin{equation} G D^{+}\left(P F_{\text {approx }}, P F_{\text {true }}\right)=\frac{1}{\left|P F_{\text {approx }}\right|} \sum_{x \in P F_{\text {approx }}} d^{+}\left(x, P F_{\text {true }}\right) \end{equation}\)

优点是比GD更能反映解是否真的“差”（即被支配）。对于那些已经达到或超越真实前沿的解，不会给予距离惩罚。但仍然需要真实帕累托前沿，计算可能比GD略复杂。

Pymoo调用实现：

from pymoo.indicators.gd_plus import GDPlus # 或者写成 GDPlus
import numpy as np

# F = np.array([[1.1, 4.9], [2.2, 2.8], [0.5, 6.0]]) # 算法找到的解集
# pf_true = np.array([[1, 5], [2, 3], [3,4], [4,1]]) # 真实帕累托前沿

# ind = GDPlus(pf_true, norm=False) # 默认p=1
# gd_plus_value = ind(F)
# print(f"GD+ (Pymoo): {gd_plus_value}")

逆时代距离IGD

IGD衡量真实帕累托前沿$P F_{\text {true }}$ 中的每个点到算法找到的近似帕累托前沿$PF_{\text {approx}}$的平均最小距离。IGD可以同时评估解集的收敛性和多样性（前提是 $P F_{\text {true }}$ 上的点分布良好且具有代表性）。IGD值越小，表示解集越好。

计算步骤：

• 确定真实的帕累托前沿$PF_{\text {true }}$：
• 确定计算解集$PF_{\text {approx}}$：
• 计算每个真实帕累托前沿解与计算解集之间的最小距离：对于 $P F_{\text {true }}$ 中的每个点 $z_j$ ，计算它与 $P F_{\text {approx }}$ 中所有解 $x_i$ 的欧氏距离，并取最小值 $d_j^{\prime} = \min_{x_i \in PF_{\text{approx}}} \operatorname{distance}\left(z_j, x_i\right)$。
• 计算所有真实帕累托前沿解的平均距离：

\[\begin{equation} I G D_p\left(P F_{\text {approx }}, P F_{\text {true }}\right)=\left(\frac{1}{\left|P F_{\text {true }}\right|} \sum_{j=1}^{\left|P F_{\text {true }}\right|}\left(d_j^{\prime}\right)^p\right)^{1 / p} \end{equation}\]

其中 $M$ 是目标数，$f_k\left(\mathbf{z}_j\right)$ 和 $f_k(\mathbf{x})$ 分别是真实前沿点 $\mathbf{z}_j$和近似解 $\mathbf{x}$ 在第 $k$ 个目标上的值。

优点：

1. 相比GD，IGD更能同时反映解集的收敛性和多样性。如果近似解集没有覆盖真实前沿的某个区域，那么该区域的真实前沿点到近似解集的最小距离会较大，从而增大IGD值。
2. 如果近似解集完全包含了真实前沿，则IGD为0。

缺点：

1. 仍然需要真实的帕累托前沿。
2. 对$P F_{\text {true }}$ 中点的数量和分布非常敏感。如果$P F_{\text {true }}$ 采样不均匀或不充分，IGD可能无法准确评估算法性能。
3. 计算成本略高于GD，因为需要遍历$P F_{\text {true }}$ 中的每个点。

代码实现：

import numpy as np

def calculate_igd(solution_set, reference_set):
    """
    计算逆世代距离 IGD。
    solution_set: (n_solutions, n_objectives) array, 算法找到的解集。
    reference_set: (n_ref_points, n_objectives) array, 真实的帕累托前沿。
    """
    solution_set = np.array(solution_set)
    reference_set = np.array(reference_set)
    
    sum_min_distances = 0.0
    for ref_point in reference_set:
        # 计算当前真实前沿点到所有近似解的欧氏距离
        distances = np.sqrt(np.sum((solution_set - ref_point)**2, axis=1))
        min_distance = np.min(distances)
        sum_min_distances += min_distance
        
    igd_value = sum_min_distances / reference_set.shape[0]
    return igd_value

# pf_approx = np.array([[1.1, 4.9], [2.2, 2.8], [3.5, 3.5], [4.2, 0.8]])
# pf_true = np.array([[1, 5], [2, 3], [3,4], [4,1]])
# igd_val = calculate_igd(pf_approx, pf_true)
# print(f"IGD: {igd_val}")

Pymoo调用实现：

from pymoo.indicators.igd import IGD
import numpy as np

# F = np.array([[1.1, 4.9], [2.2, 2.8], [3.5, 3.5], [4.2, 0.8]]) # 算法找到的解集
# pf_true = np.array([[1, 5], [2, 3], [3,4], [4,1]]) # 真实帕累托前沿

# 初始化 IGD 指标计算器
# ind = IGD(pf_true, norm=False) # Pymoo的IGD默认p=1

# 计算 IGD 值
# igd_value = ind(F)
# print(f"IGD (Pymoo): {igd_value}")

IGD+

IGD＋（Inverted Generational Distance Plus）是IGD的一个变体，类似于GD＋，它在计算 $P F_{\text {true }}$ 中的点到 $P F_{\text {approx }}$ 的距离时考虑了支配关系。对于 $P F_{\text {true }}$ 中的一个点 $z$ ，如果它支配了 $P F_{\text {approx }}$ 中的某个解 $x$ ，那么它们之间的距离就是从 $z$ 移动到 $x$ 所需的＂修正距离＂（通常是各目标分量差值之和，只考虑 $z$ 比 $x$ 好的部分）。如果 $z$ 没有支配 $P F_{a p p r o x}$ 中的任何解（即 $P F_{a p p r o x}$很好地覆盖了 $z$ 点附近区域或超越了它），则其距离为 0 。IGD＋值越小越好。 \(\begin{equation} d^{+}\left(z, P F_{\text {approx }}\right)=\min _{x \in P F_{\text {approx }}} \sqrt{\sum_{k=1}^M\left(\max \left\{0, f_k(z)-f_k(x)\right\}\right)^2} \end{equation}\) 这实际上是 $P F_{\text {true }}$ 中的点到 $P F_{\text {approx }}$ 中所有点的＂支配距离惩罚＂的最小值。 \(\begin{equation} I G D^{+}\left(P F_{\text {approx }}, P F_{\text {true }}\right)=\frac{1}{\left|P F_{\text {true }}\right|} \sum_{z \in P F_{\text {true }}} d^{+}\left(z, P F_{\text {approx }}\right) \end{equation}\)

优点：

1. 比IGD更能反映近似解集在“支配意义”上对真实前沿的覆盖程度。如果近似解集中的点能够支配或非常接近真实前沿点，则惩罚较小或为0。

缺点：

1. 仍然需要真实帕累托前沿，并对其采样敏感。计算可能比IGD略复杂。

Pymoo调用实现：

from pymoo.indicators.igd_plus import IGDPlus # 或者写成 IGDPlus
import numpy as np

# F = np.array([[1.1, 4.9], [2.2, 2.8], [0.5, 2.5]]) # 算法找到的解集
# pf_true = np.array([[1, 5], [2, 3], [3,4], [4,1]]) # 真实帕累托前沿

# ind = IGDPlus(pf_true, norm=False) # 默认p=1
# igd_plus_value = ind(F)
# print(f"IGD+ (Pymoo): {igd_plus_value}")

平均逆世代距离 (Mean Inverted Generational Distance, MIGD)：

MIGD通常指在多次独立运行同一个多目标优化算法后，计算得到的多个IGD值的平均值。它用于评估算法在多次运行中平均的收敛性和多样性表现。 \(\begin{equation} M I G D=\frac{1}{N_{\text {runs }}} \sum_{i=1}^{N_{\text {runs }}} I G D_i \end{equation}\) 其中 $N_{\text {runs }}$ 是算法的运行次数，$I G D_i$ 是第 $i$ 次运行得到的解集相对于真实前沿的IGD值。

优点：

1. 能反映算法的平均综合性能（收敛性与多样性），减少单次运行的随机性带来的影响。

缺点：

1. 需要多次运行算法，计算成本较高；依赖于真实帕累托前沿。

Pymoo本身不直接提供MIGD，需要在多次运行后手动计算平均值。

分布性指标 (Diversity/Spread Metrics)

Spacing：

Spacing（SP）指标用于衡量近似帕累托前沿$PF_{approx}$中解分布的均匀性。它计算每个解与其最近邻解之间的距离的标准差。SP值越小，表示解在近似前沿上分布越均匀。

计算步骤：

• 对于 $PF_{approx}$ 中的每个解 $x_i$，计算它与其他所有解 $x_j(j \neq i)$ 之间的距离 $d_{ij}$。
• 找到每个解 $x_i$ 的最近邻距离 $D_i = \min_{j \neq i} d_{ij}$。
• 计算这些最近邻距离的平均值$\bar{D} = \frac{1}{\lvert PF_{\mathrm{approx}} \rvert} \sum_{i=1}^{\lvert PF_{\mathrm{approx}} \rvert} D_i$。

• 计算SP： \(\begin{equation} SP = \sqrt{\frac{1}{\lvert PF_{\mathrm{approx}} \rvert - 1} \sum_{i=1}^{\lvert PF_{\mathrm{approx}} \rvert} (D_i - \bar{D})^2 } \end{equation}\)

  （有些定义中使用 $\lvert PF_{\mathrm{approx}} \rvert$ 作为分母）。理想情况下，如果所有解等距分布，则SP为0。

优点：

1. 不需要真实的帕累托前沿。
2. 能够较好地反映解的局部均匀性。

缺点：

1. 不能很好地反映解集的延展性（即是否覆盖了前沿的整个范围）。
2. 对于只有两个解的情况，SP通常是未定义的或为0，无法提供有效信息。
3. 对目标值的尺度敏感。

Pymoo调用实现：

from pymoo.indicators.spacing import Spacing as PymooSpacing # 重命名以避免与下面的Spread混淆
import numpy as np

# F = np.array([[1,5], [1.5,4], [2,3], [3,2], [4,1.5], [5,1]]) # 算法找到的解集

# ind = PymooSpacing()
# sp_value = ind(F)
# print(f"Spacing (Pymoo): {sp_value}")

最大扩展度 (Maximum Spread, MS) 或 覆盖范围 (Extent/Spread)：

这个指标衡量算法找到的近似帕累托前沿 $P F_{\text {approx }}$ 在目标空间中的延展程度。一种常见的计算方法是计算 $P F_{\text {approx }}$ 中每个目标维度的最大值和最小值之间的差，然后综合这些差值。 对于两个目标的情况，可以计算由近似前沿的极值点（例如，目标1最小的点，目标1最大的点，目标2最小的点，目标2最大的点）构成的凸包的对角线长度，或者更简单地，比较 $P F_{\text {approx }}$ 的边界框与 $P F_{\text {true }}$ 的边界框。

Pymoo 中的 MaximumSpread (来自 pymoo.indicators.ms): 它计算的是近似前沿的边界框的对角线长度与真实前沿的边界框对角线长度的比值。 \(\begin{equation} M S=\frac{\operatorname{diag}\left(B o x\left(P F_{\text {approx }}\right)\right)}{\operatorname{diag}\left(B o x\left(P F_{\text {true }}\right)\right)} \end{equation}\) 优点：

1. 能反映解集是否覆盖了帕累托前沿的广阔区域。

缺点：

1. 通常需要真实的帕累托前沿作为参考来评估覆盖程度。
2. 单独使用时，可能无法反映分布的均匀性（例如，解可能都集中在边界）。
3. 对异常值敏感。

Pymoo调用实现：

from pymoo.indicators.ms import MaximumSpread
import numpy as np

# F = np.array([[1,5], [2,3], [4,1]]) # 算法找到的解集
# pf_true = np.array([[0.5, 6], [1.5, 4], [3, 2], [5, 0.8]]) # 真实帕累托前沿

# ind = MaximumSpread(pf_true=pf_true)
# ms_value = ind(F)
# print(f"Maximum Spread (Pymoo): {ms_value}")

其他重要指标

非支配解的数量 (Number of Non-dominated Solutions, NNDS)

直接计算算法最终输出的非支配解集中的解的数量。

优点：

1. 简单直观。在某些情况下，更多的非支配解可能意味着对帕累托前沿有更丰富的近似。

缺点：

1. 数量多并不一定代表质量高。可能有很多质量差但互相非支配的解。不能反映收敛性或分布的均匀性与延展性。

直接对算法输出的解集进行非支配排序，取第一层（rank 0）的解的数量。

覆盖度 (Coverage, C-metric)

C－metric（Coverage）用于比较两个解集 $A$ 和 $B$ 的相对性能。 $C(A, B)$ 表示解集 $B$ 中有多少比例的解被解集 $A$ 中的至少一个解所帕累托支配（或相等）。 \(\begin{equation} C(A, B)=\frac{|\{\mathbf{b} \in B \mid \exists \mathbf{a} \in A, \mathbf{a} \preceq \mathbf{b}\}|}{|B|} \end{equation}\) 其中 $\mathbf{a} \preceq \mathbf{b}$ 表示 $\mathbf{a}$ 帕累托支配或等于 $\mathbf{b}_{\text {。 }}$ $C(A, B)=1$ 意味着 $A$ 中的解支配或等于 $B$ 中的所有解。 $C(A, B)=0$ 意味着 $A$ 中的解没有支配 $B$ 中的任何解。 注意 $C(A, B)$ 通常不等于 $1-C(B, A)$ 。需要同时计算 $C(A, B)$ 和 $C(B, A)$ 来全面比较。

优点：

1. 直接比较两个算法的相对优劣。

缺点：

1. 只提供相对比较，不提供绝对性能。
2. 如果两个解集不相交且互不支配，则$C(A, B)$ 和 $C(B, A)$可能都为0，无法区分。

Pymoo调用实现：

from pymoo.indicators.coverage import Coverage # Pymoo中是 CoverageIndicator
import numpy as np

# A = np.array([[1, 3], [2, 2]])
# B = np.array([[1.5, 2.5], [2.5, 1.5], [3,1]])

# 初始化 Coverage 指标计算器
# Pymoo的Coverage需要传入参考集B
# ind = Coverage(B) 
# c_A_B = ind(A) # 计算 C(A,B)
# print(f"C(A, B) (Pymoo): {c_A_B}")

# ind_B_A = Coverage(A)
# c_B_A = ind_B_A(B) # 计算 C(B,A)
# print(f"C(B, A) (Pymoo): {c_B_A}")