非支配排序遗传算法2（NSGA-II）

Posted May 19, 2025 Updated Jun 19, 2025

By Haoxiang Lu

17 min read

非支配排序遗传算法2（NSGA-II）

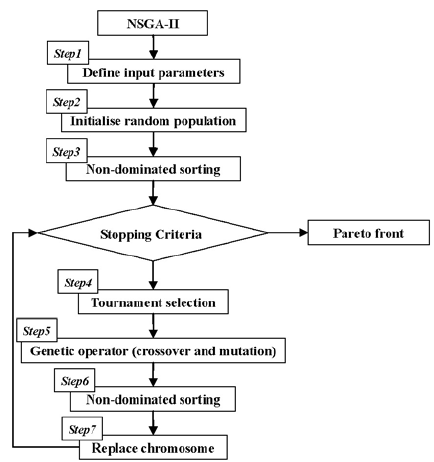
NSGA-II 是一种由GA的扩展得到的非常流行的多目标优化算法，由 Deb 等人在 2002 年提出，它保留了GA的基本框架，并加入了非支配排序和多样性维持策略，是多目标优化中的经典方法之一。它在初代 NSGA 的基础上进行了改进，主要解决了 NSGA 计算复杂度高、缺乏精英保留策略以及需要指定共享参数等问题。NSGA-II 的核心思想是基于帕累托最优概念，通过非支配排序和拥挤度计算来指导种群的进化，从而找到一组近似的帕累托最优解集。

核心概念

在理解 NSGA-II 之前，需要先了解以下几个核心概念：

多目标优化问题 (Multi-objective Optimization Problem, MOP): 与单目标优化问题不同，多目标优化问题需要同时优化两个或多个相互冲突的目标函数。例如，在汽车设计中，我们可能希望同时最小化成本和最大化燃油效率，这两个目标往往是相互制约的。一个 MOP 通常可以表示为： $\begin{equation} \begin{aligned} \text{minimize/maximize} \quad & F(x) = (f_1(x), f_2(x), \dots, f_k(x)) \\ \text{subject to} \quad & g_j(x) \le 0, \quad j = 1, \dots, m \\ & h_l(x) = 0, \quad l = 1, \dots, p \\ & x_i^L \le x_i \le x_i^U, \quad i = 1, \dots, n \end{aligned} \end{equation}$ 其中 $x$ 是决策变量向量，$F(x)$ 是目标函数向量，$g_j(x)$ 和 $h_l(x)$ 分别是不等式约束和等式约束。
非支配排序 (Non-dominated Sorting): 这是 NSGA-II 的核心步骤之一。它将种群中的所有个体分到不同的非支配层级 (fronts)。 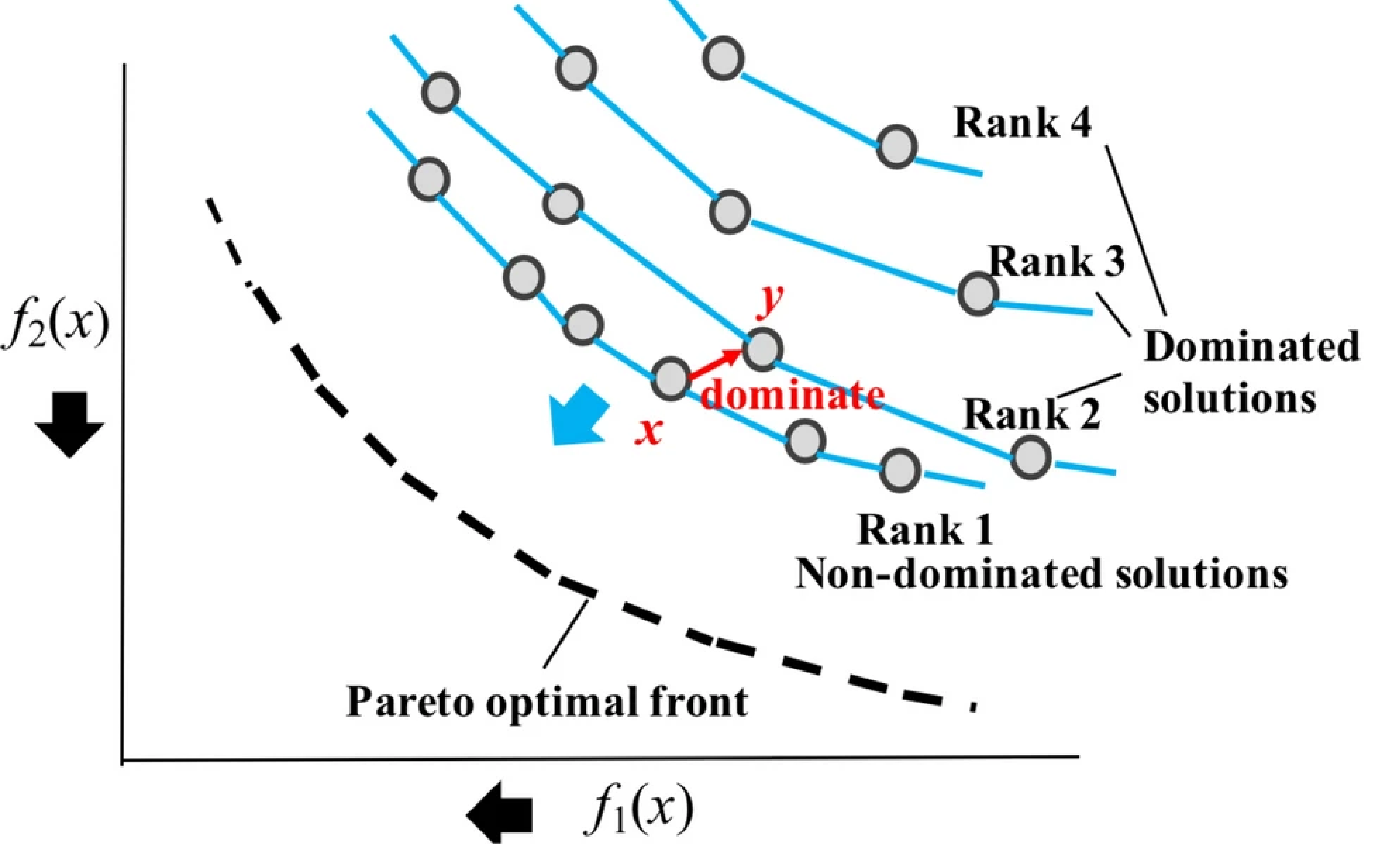非支配等级示意图
1. 第一层 (Front 1)：包含所有非支配解。
2. 第二层 (Front 2)：移除第一层解后，在剩余解中找到所有非支配解。
3. 以此类推，直到所有个体都被分配到一个层级。每个个体会被赋予一个非支配等级 (non-domination rank)，等级越低表示解越优。
拥挤度 (Crowding Distance): 当两个解具有相同的非支配等级时，拥挤度用来衡量解在其所在层级中的密度。拥挤度大的解更受欢迎，因为它有助于保持解的多样性，避免算法过早收敛到帕累托前沿的某个小区域。计算方法：
1. 对于每个目标函数，对同一层级内的个体进行排序。
2. 该层级边界上的两个个体（目标值最小和最大的个体）的拥挤度设为无穷大。
3. 对于其他个体，其拥挤度是其在该目标维度上，其左右两个邻居的目标值之差的归一化总和。具体来说，对于个体 $i$ 在目标 $m$ 上的拥挤距离分量是 $\frac{f_m(i+1) - f_m(i-1)}{f_m^{max} - f_m^{min}}$。
4. 个体的总拥挤度是其在所有目标维度上拥挤距离分量的总和。

NSGA-II 算法流程

NSGA-II算法流程图

初始化种群 $P_0$: 随机生成一个规模为 $N$ 的初始种群 $P_0$。计算 $P_0$ 中每个个体的目标函数值。
非支配排序和拥挤度计算: 对当前种群 $P_t$ (初始时为 $P_0$) 进行非支配排序，得到不同的非支配层级 $F_1, F_2, \dots$。对每个层级中的个体计算拥挤度。
选择 (Selection): 使用二元锦标赛选择进行 $N$ 次以选出 $N$ 个父代个体。每次锦标赛从种群中随机选择两个个体进行比较：
- 优先选择非支配等级较低的个体
- 如果两个体非支配等级相同，则选择拥挤度较大的个体
遗传操作 (Genetic Operators): 对选出的父代个体应用交叉和变异操作，生成一个规模为 $N$ 的子代种群 $Q_t$。
合并种群:
精英保留策略 (Elitism): 对组合种群 $R_t$ 进行非支配排序。从 $R_t$ 中选择新的父代种群 $P_{t+1}$ (规模为 $N$)：
- 按照非支配等级从低到高（即从 $F_1, F_2, \dots$）依次将整个层级的个体加入到 $P_{t+1}$ 中。
- 直到 $P_{t+1}$ 的规模达到 $N$。
- 如果加入某个层级 $F_k$ 后，$P_{t+1}$ 的规模超过 $N$，则对 $F_k$ 中的个体按照拥挤度从大到小排序，选择拥挤度较大的个体填满 $P_{t+1}$ 的剩余位置。
终止条件: 重复步骤 2-6，直到满足预设的终止条件（例如，达到最大迭代次数、帕累托前沿不再显著变化等）。

NSGA-II 的优点

计算效率高: 快速非支配排序算法的复杂度为 $O(M N^2)$ ($M$ 为目标数，$N$ 为种群大小)，优于初代 NSGA 的 $O(M N^3)$。
精英保留策略: 确保了优秀个体不会在进化过程中丢失，有助于提高收敛性。
多样性保持: 通过拥挤度计算和比较，有效维持了种群在帕累托前沿上的多样性，避免了对共享参数的依赖。
广泛应用: 是多目标优化领域最常用和最经典的算法之一。

`pymoo` 中的 NSGA-II

pymoo 是一个功能强大的 Python 多目标优化框架。它提供了各种多目标优化算法的实现，包括 NSGA-II，并且易于使用和扩展。

使用 pymoo 来运行 NSGA-II 通常包括以下步骤：

定义问题 (Problem): 你需要继承 pymoo.core.problem.Problem 类，并实现 _evaluate 方法。这个方法接收决策变量 x 作为输入，并返回目标函数值 out['F'] (以及可选的约束违反值 out['G'])。
选择算法 (Algorithm): 从 pymoo.algorithms.moo.nsga2 中导入 NSGA2 类。你可以设置算法的参数，如种群大小 (pop_size)、交叉和变异算子等。
运行优化 (Optimization): 使用 pymoo.optimize.minimize 函数来执行优化过程。你需要传入问题实例、算法实例、终止条件 (Termination) 以及其他可选参数（如是否保存历史记录 save_history，是否打印进度 verbose）。
结果分析 (Results): 优化完成后，minimize 函数会返回一个 Result 对象，其中包含了找到的非支配解集 (result.X 对应决策变量，result.F 对应目标函数值)。你可以使用 pymoo.visualization 中的工具来可视化帕累托前沿。

`pymoo` 代码示例

下面是一个使用 pymoo 中的 NSGA-II 解决一个经典双目标测试问题 ZDT1 的示例。

  
import numpy as np
from pymoo.algorithms.moo.nsga2 import NSGA2
from pymoo.problems.multi.zdt import ZDT1
from pymoo.operators.sampling.rnd import FloatRandomSampling
from pymoo.operators.crossover.sbx import SBXCrossover
from pymoo.operators.mutation.pm import PolynomialMutation
from pymoo.optimize import minimize
from pymoo.visualization.scatter import Scatter

# 1. 定义问题
# ZDT1 是一个内置问题，我们直接使用它。
# 如果是自定义问题，需要像下面这样定义：
# from pymoo.core.problem import Problem
# class MyProblem(Problem):
#     def __init__(self):
#         super().__init__(n_var=10, # 决策变量数量
#                          n_obj=2,  # 目标函数数量
#                          n_constr=0, # 约束数量
#                          xl=0.0, # 决策变量下界
#                          xu=1.0) # 决策变量上界
#     def _evaluate(self, x, out, *args, **kwargs):
#         # x 是一个 (pop_size, n_var) 的 numpy 数组
#         f1 = x[:, 0]
#         g = 1 + 9.0 / (self.n_var - 1) * np.sum(x[:, 1:], axis=1)
#         f2 = g * (1 - np.sqrt(f1 / g))
#         out["F"] = np.column_stack([f1, f2])
# problem = MyProblem()

problem = ZDT1(n_var=30) # ZDT1 问题有 30 个决策变量

# 2. 选择算法并配置参数
algorithm = NSGA2(
    pop_size=100,      # 种群大小
    n_offsprings=100,  # 每代产生的子代数量 (通常等于 pop_size)
    sampling=FloatRandomSampling(), # 初始种群生成方式
    crossover=SBXCrossover(prob=0.9, eta=15), # 模拟二进制交叉
    mutation=PolynomialMutation(eta=20),      # 多项式变异
    eliminate_duplicates=True # 消除重复个体
)

# 3. 定义终止条件
from pymoo.termination import get_termination
termination = get_termination("n_gen", 400) # 运行 400 代

# 4. 运行优化
res = minimize(problem,
               algorithm,
               termination,
               seed=1, # 设置随机种子以保证结果可复现
               save_history=True, # 保存优化历史
               verbose=True)     # 打印优化过程信息

# 5. 结果分析与可视化
# 获取帕累托前沿的解
pareto_front_X = res.X # 决策变量空间中的解
pareto_front_F = res.F # 目标函数空间中的解

print("找到的帕累托最优解的数量:", len(pareto_front_F))
# print("帕累托最优解 (目标空间):\n", pareto_front_F)

# 可视化帕累托前沿
plot = Scatter(title="ZDT1 - Pareto Front (NSGA-II)")
plot.add(problem.pareto_front(), plot_type="line", color="black", alpha=0.7, label="True Pareto Front") # 真实帕累托前沿
plot.add(pareto_front_F, color="red", s=30, label="Found Pareto Front") # 找到的帕累托前沿
plot.show()

# 如果需要查看收敛过程 (需要 matplotlib)
# try:
#     from pymoo.visualization.convergence import Convergence
#     conv = Convergence(res, problem=problem)
#     conv.plot()
#     conv.show()
# except ImportError:
#     print("matplotlib not installed. Skipping convergence plot.")

代码解释:

ZDT1(n_var=30): 加载 pymoo 内置的 ZDT1 测试问题，该问题有两个目标函数，决策变量维度为 30。
NSGA2(...): 创建 NSGA-II 算法实例。
- pop_size: 种群中个体的数量。
- n_offsprings: 每一代通过交叉和变异产生的子代数量。对于 NSGA-II，通常设置为等于 pop_size。
- sampling: 定义如何生成初始种群。FloatRandomSampling 在指定的边界内随机生成浮点数个体。
- crossover: 定义交叉算子。SBXCrossover (Simulated Binary Crossover) 是一种常用的实数编码交叉算子。prob 是交叉概率，eta 是分布指数。
- mutation: 定义变异算子。PolynomialMutation 是一种常用的实数编码变异算子。eta 是分布指数。
- eliminate_duplicates: 是否在每一代结束时移除重复的个体，有助于保持多样性。
get_termination("n_gen", 400): 设置终止条件为运行 400 代。pymoo 支持多种终止条件，如达到特定目标值、运行时间等。
minimize(...): 执行优化过程。
- problem: 定义好的问题实例。
- algorithm: 配置好的算法实例。
- termination: 终止条件。
- seed: 随机数种子，用于结果复现。
- save_history: 是否保存每一代的种群信息，用于后续分析。
- verbose: 是否在控制台打印优化进度。
res.X 和 res.F: minimize 函数返回的 Result 对象中，res.X 存储了最终一代非支配解的决策变量值，res.F 存储了它们对应的目标函数值。
Scatter(...): pymoo 提供的可视化工具，用于绘制散点图。这里用它来绘制找到的帕累托前沿和真实帕累托前沿（如果已知）。

自定义问题和算子

pymoo 的强大之处在于其灵活性。你可以轻松定义自己的优化问题，只需继承 Problem 类并实现 _evaluate 方法。同样，你也可以自定义交叉、变异、选择等算子，以适应特定问题的需求。

例如，定义一个简单的自定义问题：

  
from pymoo.core.problem import Problem
import numpy as np

class MyProblem(Problem):
    def __init__(self, n_var=2):
        # 定义问题参数：变量数，目标数，约束数，变量上下界
        super().__init__(n_var=n_var,
                         n_obj=2,
                         n_constr=0, # 可以设置约束 n_constr=1
                         xl=np.array([-5.0] * n_var),
                         xu=np.array([5.0] * n_var))

    def _evaluate(self, x, out, *args, **kwargs):
        # x 是一个 (pop_size, n_var) 的 numpy 数组
        # 计算目标函数值
        f1 = np.sum((x - 1)**2, axis=1)
        f2 = np.sum((x + 1)**2, axis=1)

        out["F"] = np.column_stack([f1, f2])

        # 如果有约束，可以这样计算并赋值：
        # g1 = x[:, 0]**2 + x[:, 1]**2 - 1  # 假设约束为 x1^2 + x2^2 <= 1
        # out["G"] = np.column_stack([g1])

然后，你可以像之前一样使用 NSGA2 和 minimize 来解决这个自定义问题。

总结

NSGA-II 是一种高效且广泛使用的多目标优化算法，它通过非支配排序和拥挤度计算来平衡解的收敛性和多样性。pymoo 库为 NSGA-II 以及其他多目标优化算法提供了便捷的 Python 实现，使得研究人员和工程师可以轻松地应用这些算法来解决实际问题。通过 pymoo，你可以方便地定义问题、配置算法、运行优化并分析结果。

Multi-Objective Optimization, Optimization Algorithm

optimization

This post is licensed under CC BY 4.0 by the author.