遗传算法(Genetic Algorithm)
遗传算法 (Genetic Algorithm, GA) 简介
遗传算法 (Genetic Algorithm, GA) 是一种借鉴生物界进化、自然选择和基因传递成功特征等理念,通过代码模拟生命过程的计算模型。它属于进化计算的一个分支,其核心思想源于达尔文的进化论。虽然我们不必精通遗传学就能使用遗传算法,但了解其基本原理有助于我们更好地理解和应用它。
在本介绍中,我们将首先回顾遗传学和生物进化过程中的一些重要概念,为后续理解遗传算法的代码模拟奠定基础,然后概述遗传算法的基本流程和关键组成部分。
达尔文进化论与遗传算法
遗传算法可以看作是自然界达尔文进化论实现的一个简化版本。达尔文进化论的核心原理可以概括为:
- 变异 (
Variation/Mutation): 种群中单个个体的特征 (也称性状或属性) 可能会有所不同,这导致了个体彼此之间存在一定程度的差异。 - 遗传 (
Heredity): 某些特征可以从亲代遗传给后代,导致后代与双亲个体具有一定程度的相似性。 - 选择 (
Selection): 在特定环境中,种群通常需要争夺有限的资源。那些更能适应环境的个体在生存竞争中更具优势,因此更有可能存活下来并产生更多的后代。
简而言之,进化过程维持了种群中个体的多样性。适应环境的个体更有可能生存、繁殖并将其优良性状传递给下一代。如此一来,随着世代的更迭,物种整体会变得更加适应其生存环境。
推动进化的重要机制包括:
- 交叉 (
Crossover) : 也称为杂交,它通过结合双亲的特征来产生后代。交叉有助于维持种群的多样性,并随着时间的推移将更优良的特征组合在一起。 - 突变 (
Mutation): 指特征的随机变异。突变通过引入偶然性的变化,在进化中也扮演着至关重要的角色。
遗传算法正是借鉴了这些思想,试图找到给定问题的最优解或近似最优解。在达尔文进化论中,保留的是种群的个体性状;而在遗传算法中,保留的是针对给定问题的一组候选解,这些候选解也被称为个体 (individuals)。这些候选解会经过迭代式的评估,用于创建下一代的解。通常,更优的解(适应度更高)有更大的机会被选中,并将其“特征”(编码的解决方案的一部分)传递给下一代候选解集合。这样,随着世代的更新,候选解集合能够更好地解决当前面临的问题。
遗传算法的核心概念
理解遗传算法需要掌握以下几个核心概念:
- 基因型 (
Genotype): 在自然界中,生物的繁殖、遗传和突变等过程都通过基因型来表征,基因型是构成染色体的一组基因的集合。在遗传算法中,每个“个体”(候选解)都由代表其基因集合的“染色体”构成。例如,一条染色体可以表示为一个二进制串,其中每个位代表一个基因。 - 种群 (
Population): 遗传算法在整个运行过程中会维持一个包含多个个体的集合,这个集合就是种群。由于每个个体都由染色体表示,因此种群可以看作是一组染色体的集合。 - 适应度函数 (
Fitness Function): 在算法的每次迭代中,都会使用适应度函数来评估种群中每个个体的优劣程度。目标函数是遗传算法试图优化或解决的问题的数学表达。适应度得分越高的个体代表了越好的解,它也就更有可能被选择用于繁殖,并将其性状在下一代中得到表现。随着遗传算法的进行,解的质量通常会提高,适应度会增加。一旦找到具有令人满意的适应度值的解,就可以终止遗传算法。 - 选择 (
Selection): 在计算出种群中每个个体的适应度之后,选择过程会根据适应度值来确定种群中的哪些个体将被用于繁殖并产生下一代。通常,具有较高适应度值的个体更有可能被选中,并将其遗传物质传递给下一代。然而,为了保持种群的多样性,适应度较低的个体仍然有一定概率被选中,这样它们的遗传物质就不会被完全摒弃。 - 交叉 (
Crossover): 为了创建新的个体(后代),交叉操作会将从当前代中选择出来的两个亲代个体的染色体片段进行互换。这样就产生了两个新的染色体,代表了它们的后代。 - 突变 (
Mutation): 突变操作的目的是定期地、随机地改变种群中个体的基因,从而将新的模式引入染色体,并鼓励算法在解空间的未知区域进行搜索。突变可以表现为基因的随机变化,例如,在二进制串表示的染色体中,随机翻转某一位的值(0变1或1变0)。
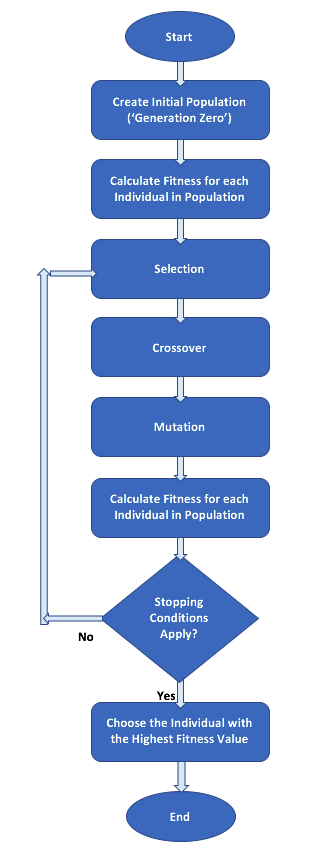
遗传算法的基本流程
遗传算法通常遵循以下基本步骤:
创建初始种群 (Initialization) 初始种群是一组随机生成的、针对当前问题的有效候选解(个体)。由于遗传算法使用染色体代表每个个体,因此初始种群实际上是一组染色体的集合。
计算适应度 (Fitness Calculation/Evaluation) 对种群中的每个个体,使用预定义的适应度函数计算其适应度值。对于初始种群,此操作将执行一次。在后续的每一代中,当通过选择、交叉和突变等遗传算子产生新一代个体后,都需要重新计算新个体的适应度。由于每个个体的适应度计算通常独立于其他个体,因此这个过程具备并行计算的潜力。 值得注意的是,选择阶段通常倾向于适应度得分较高的个体。因此,遗传算法本质上是朝着最大化适应度得分的方向进行搜索。如果实际问题是求解最小值,那么在适应度计算时需要对原始目标函数值进行转换,例如将其乘以 -1,或者取其倒数(并处理可能出现的除零问题)。
- 应用遗传算子:选择、交叉和变异 (Selection, Crossover, and Mutation) 将选择、交叉和突变这三个核心的遗传算子按特定顺序和概率应用到当前种群中,从而产生新一代的种群。新一代种群通常会继承当前代中较优个体的特征。
- 选择 (
Selection): 此操作负责从当前种群中挑选出有优势的个体进入“交配池”(mating pool),准备进行繁殖。 - 交叉 (
Crossover): 此操作从选定的父代个体创建后代。这通常是通过交换两个被选定的父代个体染色体的一部分来完成的,从而创建代表后代的两个新染色体。 - 突变 (
Mutation): 此操作会对新创建的(子代)个体的一个或多个染色体值(基因)进行随机的小幅改变。突变发生的概率通常设置得非常低,以避免破坏已经学习到的优良模式,同时又能引入新的遗传多样性。
- 选择 (
- 算法终止条件 (Termination Condition) 在确定算法是否应该停止时,可以使用多种条件进行检查。两种最常用的停止条件是:
- 达到预设的最大世代数 (Maximum Number of Generations): 这是一个常用的限制,用于控制算法的运行时间和计算资源消耗。
- 解的质量收敛 (Convergence): 即在过去的若干代中,种群中最优个体的适应度没有明显改进。这可以通过记录每一代获得的最优适应度值,然后将当前的最优值与预定数量的几代之前获得的最优值进行比较来实现。如果它们之间的差异小于某个预设的阈值,则可以认为算法已经收敛,可以停止。
完成上述步骤后,如果未达到终止条件,则新的种群将替代旧的种群,并从第2步(计算适应度)开始重复该过程。这个迭代过程会一直持续,直到满足终止条件为止。算法最终输出的是迄今为止找到的适应度最高的个体,作为问题的最优解或近似最优解。
遗传算法的超参数
遗传算法的性能在很大程度上受到其各种参数设置(即超参数)的影响。通过调整这些超参数和遗传算子的具体实现方式,可以优化解的进化过程。以下是一些常见的超参数及其作用:
- 种群大小 (
Population Size): 表示每一代进化模拟中包含的个体数量。种群大小通常与染色体的复杂性(如基因序列的长度)相关。对于具有更复杂基因序列的个体,可能需要更大的种群才有机会进化出高适应度的个体。 - 世代数 (
Number of Generations): 类似于深度学习中的epoch,世代数表示遗传算法进化的迭代次数。在遗传算法中,每一代都需要进化整个种群。合适的世代数通常由染色体的长度、复杂性以及问题的难度决定。世代数可以与种群大小进行权衡,例如,可以使用较大的种群和较少的世代数,反之亦然。 - 交叉率 (
Crossover Rate): 指在每一代中执行交叉操作的个体所占的比例,或者用于确定交叉点的位置或数量的参数。较高的交叉率意味着更多的个体将参与重组,这有助于探索新的解空间区域,但也可能破坏已有的优良模式。 - 突变率 (
Mutation Rate): 指个体中每个基因发生突变的可能性。较高的突变率通常会导致种群发生较多的变异,这可能有利于解决复杂或多峰值的优化问题,帮助算法跳出局部最优。然而,过高的突变率也可能阻碍个体向最优解收敛,使得搜索过程变得不稳定。相反,较低的突变率会产生较少的种群变异,可能导致算法过早收敛到局部最优。
遗传算法为更广泛的进化计算 (Evolutionary Computation, EC) 方法奠定了基础。从根本上讲,进化和“适者生存”的概念是所有进化计算方法的关键组成部分。