Bootstrap 重采样方法

Bootstrap 方法

Bootstrap 的核心思想与基本步骤 (Core Idea and Basic Steps)

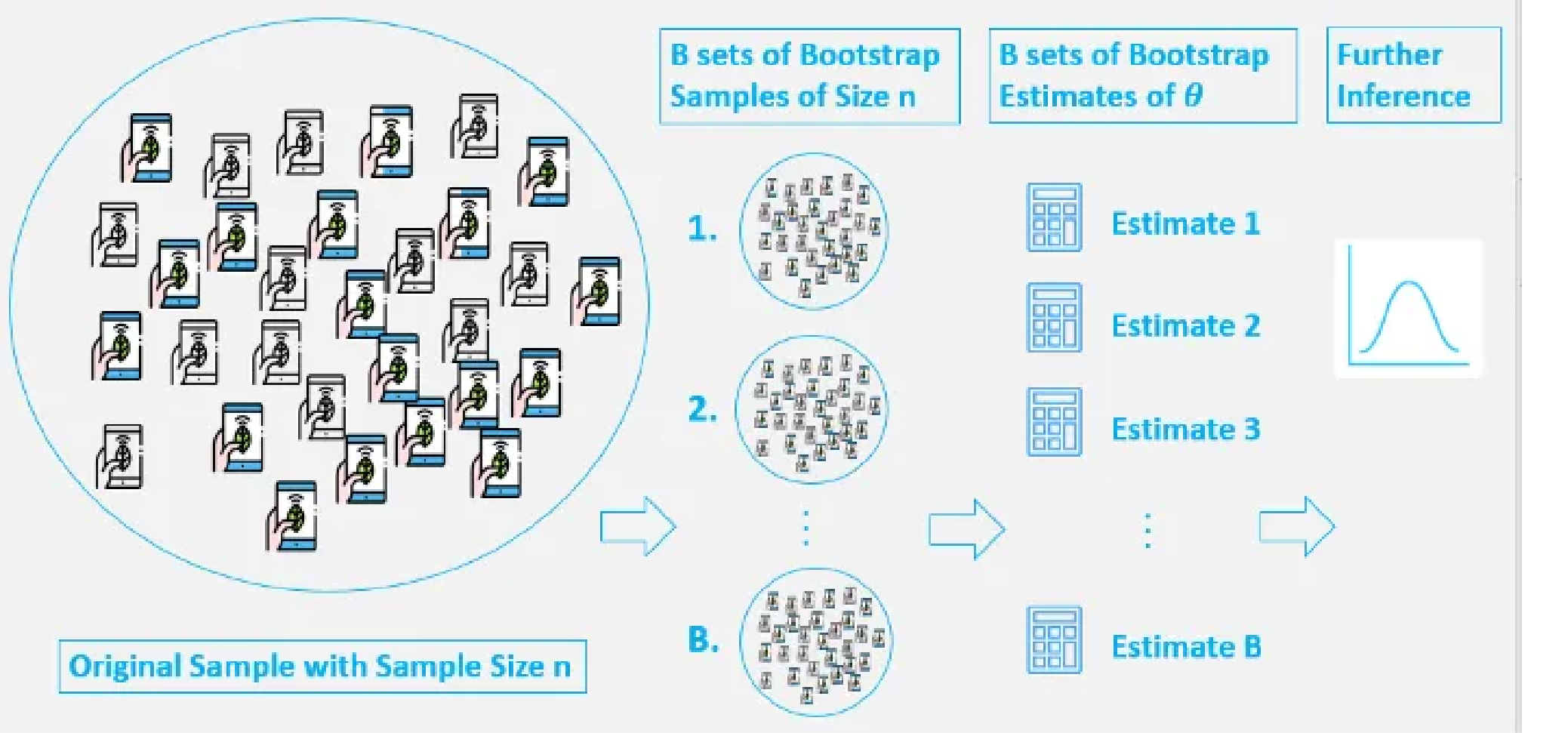
Bootstrap 方法，正如其名”自举”，灵感来源于”拔着自己的鞋带把自己提起来”的荒诞故事，由 Efron 在1979年提出。其核心思想是：在只有一个样本、且对总体分布知之甚少的情况下，将这个已有的样本数据（经验分布函数 EDF）视为对真实总体分布的最佳近似。然后，通过对这个”近似总体”进行有放回的重复抽样 (resampling with replacement) 来模拟多次独立采样的过程，从而估计我们关心的总体参数 $ \theta $ (例如总体均值、中位数、方差等) 的估计值 (例如样本均值、样本中位数等) 的性质，如其抽样分布、标准误或置信区间。

这是一种重采样方法，从具有相同样本量 $ n $ 的现有样本数据中独立地进行有放回采样，并在这些重采样数据中进行推断。

基本步骤

1. 原始样本 (Original Sample): 我们有一个从未知总体中抽取的、包含 $ n $ 个观测值的原始样本 $ S = {x_1, x_2, …, x_n} $。
2. 有放回重采样 (Resampling with Replacement): 从原始样本 $ S $ 中有放回地随机抽取 $ n $ 个观测值，形成一个新的样本，称为自助样本 (Bootstrap Sample) $ S^* $。由于是有放回抽样，$ S^* $ 中的某些原始观测值可能会出现多次，而另一些可能一次也不出现。
3. 计算统计量 (Calculate Statistic): 对每个自助样本 $ S^* $ 计算我们感兴趣的统计量 $ \hat{\theta}^* $ (例如均值、中位数、方差、相关系数等)。
4. 重复 (Repeat): 重复步骤 2 和步骤 3 大量次数 (例如 B 次，通常 B 至少为 1000，甚至更多，如10000次，以获得更稳定的结果)，得到 B 个自助统计量 \(\hat{\theta}^*_1, \hat{\theta}^*_2, ..., \hat{\theta}^*_B\)。
5. 统计推断 (Statistical Inference): 用这 B 个 Bootstrap 统计量 \(\{\hat{\theta}^*_1, ..., \hat{\theta}^*_B\}\) 构建一个经验抽样分布。这个分布被用作对真实统计量 \(\hat{\theta}\) 抽样分布的近似。基于这个分布，我们可以：
   • 估计统计量 $ \hat{\theta} $ 的标准误 (Standard Error, SE)。
   • 构建统计量 $ \hat{\theta} $ 的置信区间 (Confidence Interval, CI)。
   • 进行假设检验 (Hypothesis Testing)。

核心类比: “子样本之于样本，可以类比样本之于总体。” (Sub-sample is to sample, as sample is to population.) Bootstrap 的巧妙之处就在于，它用从样本中再抽样的变异性来模拟从总体中抽样的变异性。

引入 Bootstrap 的初衷及目的 (Original Motivation and Objectives)

• 估计标准误 (Standard Error Estimation): 许多统计量的标准误在解析上难以推导，特别是对于复杂的统计量（如中位数、分位数、相关系数、回归系数的某些非标准估计）。Bootstrap 提供了一种通用的、基于模拟的数值计算方法。
• 构建置信区间 (Confidence Interval Construction): 当数据的潜在分布未知或不符合经典统计方法（如t检验、Z检验）的正态性假设时，或者当样本量较小时，Bootstrap 可以构建更可靠的置信区间。
• 进行假设检验 (Hypothesis Testing): 虽然不如前两者常用，但 Bootstrap 的思想也可以用于构建非参数的假设检验。
• 减少对分布假设的依赖: 作为一种非参数或半参数方法（取决于具体实现），Bootstrap 放宽了对总体分布形式的严格要求。
• 处理小样本问题: 传统依赖大样本理论的方法在小样本下可能失效，Bootstrap 提供了一种替代方案。
• 评估模型稳定性和预测不确定性: 在机器学习中，如 Bagging (Bootstrap Aggregating) 技术，就是利用 Bootstrap 来提高模型的稳定性和准确性。

Bootstrap 的类型

非参数 Bootstrap (Non-parametric Bootstrap)

这是最常见的 Bootstrap 形式，其过程如基本步骤所述。它不假定总体分布的具体形式，而是直接从原始样本的经验分布函数 (EDF) 中进行重采样。

• 估计量的标准误差的 Bootstrap 估计: 设 \(\hat{\theta}\) 是基于原始样本 \(x_1, ..., x_n\) 计算得到的参数 \(\theta\) 的估计量。我们生成 B 个 Bootstrap 样本，并为每个样本计算相应的 Bootstrap 估计 \(\hat{\theta}_1^*, \hat{\theta}_2^*, ..., \hat{\theta}_B^*\)。 标准误的 Bootstrap 估计 \(\hat{SE}_{boot}(\hat{\theta})\) 可以计算为这些 Bootstrap 估计的标准差：

  \[\begin{equation} \hat{SE}_{boot}(\hat{\theta}) = \sqrt{\frac{1}{B-1} \sum_{i=1}^B (\hat{\theta}_i^* - \bar{\theta}^*)^2} \end{equation}\]

  其中 $ \bar{\theta}^* = \frac{1}{B} \sum_{i=1}^B \hat{\theta}_i^* $ 是 Bootstrap 估计的均值。

• 估计量的均方误差 (MSE) 的 Bootstrap 估计: 如果我们关心的是估计量 $ \hat{\theta} $ 相对于真实参数 $ \theta $ 的均方误差 $ MSE_F(\hat{\theta}) = E_F[(\hat{\theta} - \theta)^2] $，Bootstrap 可以提供一个近似估计。一种常见的方法是估计 $ E_{F_n}[(\hat{\theta}^* - \hat{\theta})^2] $，即：

  \[\begin{equation} \hat{MSE}_{boot} = \frac{1}{B} \sum_{i=1}^B (\hat{\theta}_i^* - \hat{\theta})^2 \end{equation}\]

  其中 $ \hat{\theta} $ 是原始样本的估计值。这实际上估计的是方差加上偏差的平方的一个近似。

• Bootstrap 置信区间 (Percentile Method): 这是构建置信区间最直接的方法之一。

  1. 获得 B 个 Bootstrap 估计 \(\hat{\theta}_1^*, \hat{\theta}_2^*, ..., \hat{\theta}_B^*\)。
  2. 将这些估计值从小到大排序: \(\hat{\theta}_{(1)}^* \le \hat{\theta}_{(2)}^* \le ... \le \hat{\theta}_{(B)}^*\)。
  3. 对于一个置信水平为 $ 1-\alpha $ 的置信区间，找出排序后的第 $ k_1 = \lfloor B \times (\alpha/2) \rfloor $ 个值和第 $ k_2 = \lceil B \times (1-\alpha/2) \rceil $ 个值 (或者更简单地取 $ B \times (\alpha/2) $ 和 $ B \times (1-\alpha/2) $ 百分位数)。
  4. 则 \((\hat{\theta}_{(k_1)}^*, \hat{\theta}_{(k_2)}^*)\) 即为 \(\theta\) 的 \(1-\alpha\) Bootstrap 百分位置信区间。 例如，对于 95% 置信区间 (\(\alpha = 0.05\)), 我们会取第 2.5 百分位数和第 97.5 百分位数。

参数 Bootstrap (Parametric Bootstrap)

当我们可以对总体的分布函数 $ F(x; \beta) $ 的形式做出假设，但其中的参数 $ \beta $ (可以是向量) 未知时，可以使用参数 Bootstrap。

步骤如下：

1. 估计参数: 利用原始样本 $ X_1, X_2, …, X_n $ 估计未知参数 $ \beta $，得到估计值 $ \hat{\beta} $ (例如，通过最大似然估计)。
2. 生成参数 Bootstrap 样本: 从已拟合的参数分布 \(F(x; \hat{\beta})\) 中生成 B 个容量为 \(n\) 的新样本。每个这样的样本 \(X_1^*, ..., X_n^*\) 都是从 \(F(x; \hat{\beta})\) 中随机抽取的。
3. 计算统计量: 对每个参数 Bootstrap 样本计算感兴趣的统计量 $ \hat{\theta}^* $。
4. 统计推断: 使用这 B 个 $ \hat{\theta}^* $ 构建经验抽样分布，后续步骤与非参数 Bootstrap 类似（计算标准误、置信区间等）。

参数 Bootstrap 的有效性依赖于所选参数模型 $ F(x; \beta) $ 对真实数据生成过程的拟合程度。如果模型选择不当，结果可能会有偏。

Bootstrap 与标记重捕法 (Mark-Recapture) 的区别

特征	Bootstrap	标记重捕法 (Mark-Recapture)
主要目的	估计任意统计量的抽样分布、标准误、置信区间等。	主要用于生态学中估计封闭种群的个体数量 (Population Size Estimation)。
数据来源	基于一个已获得的样本数据。	基于对真实总体的至少两次实际捕捉和观察。
“重采样”含义	从原始样本中有放回地重复抽样，生成自助样本（计算机模拟）。	指对总体的重复捕捉事件，观察标记个体的比例（实际野外操作）。
应用领域	统计学、机器学习、计量经济学等广泛领域。	主要在生态学、野生动物管理。

Bootstrap 与蒙特卡洛方法 (Monte Carlo Methods) 的区别

蒙特卡洛方法是一个更广泛的计算技术类别，依赖于重复的随机抽样来获得数值结果。Bootstrap 可以视为蒙特卡洛方法的一种特定应用，其特殊之处在于它是从数据的经验分布函数 (EDF) 中进行抽样。

特征	Bootstrap	蒙特卡洛方法 (General Monte Carlo)
核心思想	从观测数据的经验分布函数 (EDF) 中有放回抽样。	基于大量随机抽样和统计试验来获取数值近似解。
数据生成来源	基于现有样本数据进行有放回的重抽样（从原始样本中”复制”数据）。严重依赖原始样本的质量和代表性。	通常从一个已知的或假设的理论概率分布中生成新数据（如正态分布、均匀分布等）。不需要原始数据，只需要分布假设。
主要目的	统计推断：估计统计量的性质 (标准误、置信区间)。	更广泛：数值积分、模拟复杂系统、优化、贝叶斯推断中的后验抽样等。
对总体的假设	原始样本是总体的一个良好代表。	可以直接模拟一个已知的总体分布，或探索可通过随机过程描述的系统。

应用场景对比:

问题类型	蒙特卡洛模拟 (General)	Bootstrap
已知理论分布	✔️ 直接从理论分布生成数据。	❌ (非参数Bootstrap不依赖理论分布假设) / ✔️ (参数Bootstrap基于拟合的理论分布)
未知分布（只有样本）	❌ (除非先对样本拟合一个分布再模拟)	✔️ 直接从样本的经验分布中重抽样。
高维积分	✔️ (常用方法，如重要性采样)	❌ (主要不用于此)
统计量置信区间	❓ (如果知道统计量的分布可以，否则难)	✔️ 主要应用之一，无需分布假设即可估计。
小样本问题	❓ (取决于分布假设的准确性)	✔️ 通过重抽样”放大”样本信息，常用于小样本推断。

Python 实现 (Python Implementation)

基于 numpy 的手动实现

import numpy as np

def bootstrap_statistic_manual(data, statistic_func, n_iterations=1000):
    """
    手动执行 Bootstrap 过程来估计某个统计量的分布。
    """
    n_size = len(data)
    bootstrap_stats = []
    for _ in range(n_iterations):
        bootstrap_sample = np.random.choice(data, size=n_size, replace=True)
        stat = statistic_func(bootstrap_sample)
        bootstrap_stats.append(stat)
    return bootstrap_stats

# 示例数据
original_sample = np.array([2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 5, 8, 10])
print(f"原始样本: {original_sample}")
original_mean = np.mean(original_sample)
print(f"原始样本均值: {original_mean:.2f}")

# 手动 Bootstrap 均值
bootstrap_means_manual = bootstrap_statistic_manual(original_sample, np.mean, n_iterations=10000)
std_error_mean_manual = np.std(bootstrap_means_manual, ddof=1)
# 百分位置信区间
alpha = 0.05
lower_manual = np.percentile(bootstrap_means_manual, 100 * (alpha / 2))
upper_manual = np.percentile(bootstrap_means_manual, 100 * (1 - alpha / 2))

print(f"\n--- 手动 Numpy 实现 (均值) ---")
print(f"Bootstrap 估计的标准误: {std_error_mean_manual:.2f}")
print(f"95% 百分位置信区间: [{lower_manual:.2f}, {upper_manual:.2f}]")

使用 scipy.stats.bootstrap

scipy提供了 scipy.stats.bootstrap 函数，可以非常方便地执行 Bootstrap 分析。

scipy.stats.bootstrap(data, statistic, *, n_resamples=9999, confidence_level=0.95, method='BCa', random_state=None, axis=0, batch=None)

主要参数说明：

• data: 一个或多个样本数据序列。如果是单个样本，可以是一维数组。如果是多个样本（例如用于比较两个独立样本的统计量差异），可以是一个包含多个一维数组的元组或列表。
• statistic: 一个可调用对象 (函数)，它接收 data (或从 data 中抽样的样本) 作为参数并返回计算得到的统计量。该函数必须能处理 axis 参数 (如果 data 是多维的或用于多样本情况)。
• n_resamples: Bootstrap 重采样的次数。默认 9999。
• confidence_level: 置信区间的置信水平。默认 0.95 (即 95% 置信区间)。
• method: 计算置信区间的方法。常用的有：
  • 'percentile': 百分位法 (我们之前手动实现的)。
  • 'basic': 基本 Bootstrap 法 (也称枢轴量法)。
  • 'BCa': 偏差校正和加速 (Bias-Corrected and accelerated) Bootstrap 法。这通常被认为是更准确的方法，特别是对于有偏的统计量或非对称分布，是 scipy 的默认方法。
• random_state: 用于控制随机数生成的可复现性。可以是一个整数或 np.random.Generator 实例。
• axis: 如果 data 是多维数组，指定沿哪个轴计算统计量。
• batch: 如果提供，则以批处理方式执行重采样，可以节省内存，但可能会稍慢。

返回值: 一个 BootstrapResult 对象，包含以下主要属性：

• confidence_interval: 一个 ConfidenceInterval 对象，包含 low 和 high 属性，表示置信区间的下限和上限。
• standard_error: Bootstrap 估计的标准误。
• bootstrap_distribution: (可选，如果 method 支持且未用 batch) 所有 Bootstrap 统计量的数组。

示例代码:

from scipy import stats
import numpy as np

# 示例数据
original_sample = np.array([2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 5, 8, 10])
n_resamples = 10000 # 保持与手动一致

print(f"\n--- Scipy 实现 (均值) ---")
# 对于单样本统计量，statistic 函数通常接收一个样本
# data 需要是 (sample,) 的形式或者是一个包含单个样本的列表/元组
# scipy.stats.bootstrap 希望 data 是一个序列的序列，即使只有一个样本
data_for_scipy = (original_sample,) 

# 估计均值的置信区间和标准误
# 使用 BCa 方法 (默认)
res_mean_bca = stats.bootstrap(data_for_scipy, np.mean, n_resamples=n_resamples, random_state=42)
print(f"BCa 方法 95% 置信区间 (均值): [{res_mean_bca.confidence_interval.low:.2f}, {res_mean_bca.confidence_interval.high:.2f}]")
print(f"BCa 方法估计的标准误 (均值): {res_mean_bca.standard_error:.2f}")

# 使用百分位法
res_mean_percentile = stats.bootstrap(data_for_scipy, np.mean, method='percentile', n_resamples=n_resamples, random_state=42)
print(f"Percentile 方法 95% 置信区间 (均值): [{res_mean_percentile.confidence_interval.low:.2f}, {res_mean_percentile.confidence_interval.high:.2f}]")
print(f"Percentile 方法估计的标准误 (均值): {res_mean_percentile.standard_error:.2f}")


print(f"\n--- Scipy 实现 (中位数) ---")
# 估计中位数的置信区间和标准误
res_median_bca = stats.bootstrap(data_for_scipy, np.median, n_resamples=n_resamples, random_state=42)
print(f"BCa 方法 95% 置信区间 (中位数): [{res_median_bca.confidence_interval.low:.2f}, {res_median_bca.confidence_interval.high:.2f}]")
print(f"BCa 方法估计的标准误 (中位数): {res_median_bca.standard_error:.2f}")

res_median_percentile = stats.bootstrap(data_for_scipy, np.median, method='percentile', n_resamples=n_resamples, random_state=42)
print(f"Percentile 方法 95% 置信区间 (中位数): [{res_median_percentile.confidence_interval.low:.2f}, {res_median_percentile.confidence_interval.high:.2f}]")
print(f"Percentile 方法估计的标准误 (中位数): {res_median_percentile.standard_error:.2f}")

# 示例：比较两个独立样本均值的差异
sample1 = np.array([1, 2, 3, 4, 5, 6])
sample2 = np.array([3, 5, 7, 9])

def diff_means(s1, s2, axis=0): # statistic function needs to handle axis for multi-sample input
    return np.mean(s1, axis=axis) - np.mean(s2, axis=axis)

data_two_samples = (sample1, sample2)
res_diff_means = stats.bootstrap(data_two_samples, diff_means, n_resamples=n_resamples, random_state=42)
print(f"\n--- Scipy 实现 (两独立样本均值差) ---")
print(f"原始样本均值差: {np.mean(sample1) - np.mean(sample2):.2f}")
print(f"BCa 方法 95% 置信区间 (均值差): [{res_diff_means.confidence_interval.low:.2f}, {res_diff_means.confidence_interval.high:.2f}]")
print(f"BCa 方法估计的标准误 (均值差): {res_diff_means.standard_error:.2f}")

注意:

• 当向 stats.bootstrap 传递单个样本时，data 参数通常期望是一个包含该样本的元组或列表，例如 (original_sample,) 或 [original_sample]。这是因为该函数设计为可以处理多个样本（例如，比较两个样本的均值差）。
• 传递给 statistic 的函数应该能够接受通过 axis 参数指定的轴上的操作，特别是当处理多维数据或多样本情况时。对于 np.mean, np.median 等NumPy函数，它们本身就支持 axis 参数。

Bootstrap 的应用和优势与局限性

应用非常广泛，包括：

• 估计均值、中位数、方差、相关系数、回归系数等的标准误和置信区间。
• 在A/B测试中比较两组或多组之间的差异，特别是当数据分布不规则或样本量小时。
• 机器学习中的 Bagging (如随机森林)、模型参数的稳定性评估。
• 金融中的风险价值 (VaR)、预期损失 (Expected Shortfall) 的估计。
• 生物信息学中的系统发育树的置信度评估。

优势:

• 通用性强: 可以应用于各种统计量，包括那些没有简单解析表达式的标准误或抽样分布的统计量（如中位数、百分位数、Kendall’s tau 等）。
• 减少分布假设: 非参数 Bootstrap 对总体分布的假设非常宽松，仅要求样本是独立同分布的。
• 概念简单，易于实现: 基本思想直观，编程实现相对容易。
• 处理复杂估计量: 对于复杂的模型参数或统计量，Bootstrap 往往是少数可行的推断方法之一。
• 通常表现良好: 在许多情况下，尤其是有足够大的原始样本时，Bootstrap 提供的标准误和置信区间是相当准确的。

局限性:

• 计算密集型: 需要大量的重复抽样和计算，对于非常大的数据集或复杂的统计量计算可能耗时较长。
• 依赖原始样本的质量: Bootstrap 的结果高度依赖于原始样本对总体的代表性。如果原始样本有偏或包含异常值，Bootstrap 结果也可能受到影响。所谓”垃圾进，垃圾出”。
• 小样本问题: 虽然常用于小样本，但如果原始样本过小，其经验分布可能无法很好地代表总体分布，导致 Bootstrap 结果不稳定或有偏。
• 对极值的估计可能不佳: 对于依赖数据分布尾部信息的统计量（如极值），Bootstrap 可能表现不佳。
• 可能过于乐观: 有时，特别是在小样本情况下，Bootstrap 置信区间可能比真实的置信区间更窄（即过于乐观）。
• 并非万能: 对于某些问题，例如估计总体参数的边界 (如均匀分布的最大值)，标准 Bootstrap 可能失效。需要特定的变种或调整。
• 选择 Bootstrap 方法: 存在多种 Bootstrap 置信区间构建方法 (Percentile, Basic, BCa, Studentized Bootstrap)，它们在不同情况下的性能各异。BCa 通常被认为是较好的选择，但计算也更复杂。

总结

Bootstrap 是一种强大且灵活的统计工具，它通过计算机模拟的力量，使得我们能够对各种统计量的性质进行推断，而无需对数据做过多的参数假设。它在现代统计学和数据科学中扮演着越来越重要的角色。理解其原理、适用场景以及潜在的局限性，对于正确和有效地应用它至关重要。scipy 等库的出现使得 Bootstrap 的应用变得更加便捷。