自适应神经模糊推理系统(ANFIS)
自适应神经模糊推理系统(Adaptive Neuro-Fuzzy Inference System, ANFIS)融合了神经网络和模糊逻辑,由 Jyh-Shing Roger Jang 于 1993 年首次提出。它结合模糊推理系统的可解释性和神经网络的自适应学习能力,通过模糊规则和神经网络的训练机制,构建输入与输出之间的映射关系。ANFIS 擅长处理不确定性和非线性问题,可对输入与输出的复杂关系进行建模。
ANFIS 的原理
模糊推理系统(FIS)
模糊推理系统(Fuzzy Inference System, FIS)是 ANFIS 的核心基础,基于模糊逻辑来模拟人类决策过程。典型 FIS 包含以下步骤:
- 模糊化(Fuzzification):将精确输入转换为模糊集合,使用隶属函数(如高斯)计算隶属度。
- 模糊规则(Fuzzy Rules):定义输入与输出之间的模糊关系。
- 模糊推理(Fuzzy Inference):根据规则推导模糊输出。
- 去模糊化(Defuzzification):将模糊输出转化为精确值。
FIS 擅长处理模糊数据,但参数通常需要人工设定,缺乏自适应性。
神经网络
神经网络是一种数据驱动的学习模型,通过多层神经元和权重更新来拟合输入与输出的关系,善于从数据中提取模式,但可解释性较弱。
ANFIS 的结合
ANFIS 将模糊推理系统的计算过程结构化为神经网络形式,并利用神经网络的学习能力来优化模糊规则的参数:
- 隶属函数参数(前提参数)与规则输出参数(后件参数)都可训练。
- 通过混合学习算法(结合反向传播和最小二乘法),自动调整这些参数以适应数据。
这种方式兼具模糊逻辑的可解释性和神经网络的自适应性。
ANFIS 的结构
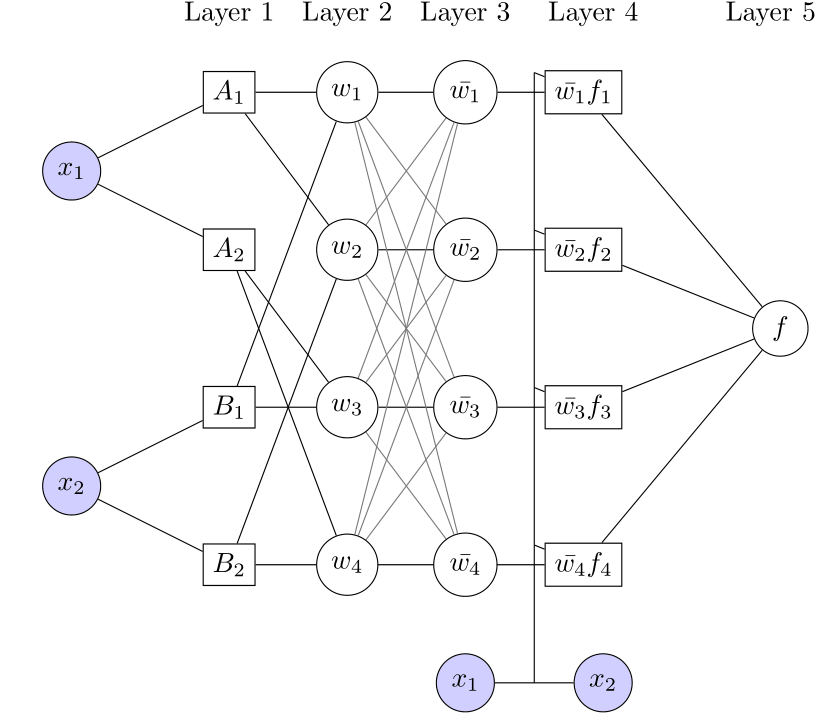
ANFIS 的网络结构分为五层,每层对应模糊推理系统的一个步骤:
- 模糊层(Layer 1)
- 功能:对输入进行模糊化。
- 数学表达式:对于输入 $x$,输出为 $O_{1,i} = \mu_{A_i}(x)$,其中 $\mu_{A_i}(x)$ 为前提参数。
- 规则层(Layer 2)
- 功能:计算每条模糊规则的触发强度。
- 数学表达式:对于规则 $i$,触发强度 $w_i = \mu_{A_i}(x) \cdot \mu_{B_i}(y)$。
- 归一化层(Layer 3)
- 功能:对规则触发强度进行归一化。
- 数学表达式:$\bar{w}_i = \frac{w_i}{\sum w_j}$。
- 去模糊化层(Layer 4)
- 功能:计算每条规则的输出,通常为线性函数的组合。
- 数学表达式:$\bar{w}_i f_i = \bar{w}_i (p_i x + q_i y + r_i)$,其中 $p_i, q_i, r_i$ 为后件参数。
- 总输出层(Layer 5)
- 功能:汇总所有规则输出。
- 数学表达式:$f = \sum \bar{w}_i f_i$。
ANFIS 的训练
ANFIS 使用 混合学习算法(结合反向传播和最小二乘法)分两个阶段训练:
- 前向传播:固定前提参数,用最小二乘法求解后件参数。
- 反向传播:固定后件参数,用梯度下降优化前提参数。
这种模式兼顾了训练效率和准确度。
ANFIS 的应用
ANFIS 应用于自动控制、信号处理、时间序列预测以及分类等多个领域。
- 自动控制:如机器人控制、空调调节。
- 信号处理:如语音识别、噪声滤波。
- 时间序列预测:如天气预报、股票预测。
- 分类与诊断:如医学诊断、故障检测。
例如在自动驾驶中,ANFIS 可根据模糊输入(如“距离近”、“速度快”)来平滑控制刹车力度。
使用 Python 实现 ANFIS
下面基于 anfis 库演示如何拟合正弦函数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import numpy as np
import anfis
from anfis import membership
from anfis import mfDerivs
import matplotlib.pyplot as plt
# 生成训练数据
x = np.linspace(0, 10, 100) # 输入范围 [0, 10]
y = np.sin(x) # 目标输出 sin(x)
# 定义隶属函数
mf = [[['gaussmf', {'mean': 0., 'sigma': 1.}],
['gaussmf', {'mean': 5., 'sigma': 1.}],
['gaussmf', {'mean': 10., 'sigma': 1.}]]]
# 创建 ANFIS 模型
model = anfis.ANFIS(n_inputs=1, n_rules=3, mf=mf)
# 训练模型
model.trainHybridJangOffLine(epochs=10, X=x.reshape(-1, 1), Y=y.reshape(-1, 1))
# 预测
y_pred = model.predict(x.reshape(-1, 1))
# 可视化
plt.plot(x, y, 'b-', label='真实值')
plt.plot(x, y_pred, 'r--', label='预测值')
plt.xlabel('x')
plt.ylabel('y')
plt.title('ANFIS 拟合正弦函数')
plt.legend()
plt.grid(True)
plt.show()
代码说明
- 数据:输入 $x$ 和目标输出 $y = \sin(x)$。
- 隶属函数:定义三个高斯函数,中心分别为 0、5、10。
- 训练:使用混合学习算法训练 10 个周期。
- 结果:可视化真实值与预测值的对比。
ANFIS 的优点和局限性
优点
- 处理不确定性:适用于模糊或不精确数据。
- 混合优势:融合模糊逻辑与神经网络的特性。
- 自适应性:自动优化参数。
局限性
- 数据依赖:需要足够的训练数据。
- 易过拟合:模型复杂度可能造成过拟合。
- 计算开销:高维输入提高计算复杂度。
- 单输出限制:ANFIS 仅支持单变量输出。
ANFIS相关工作
- S-ANFIS:S-ANFIS 是 ANFIS 网络的简单推广,其中模型前提和结果部分的输入可以分别控制。
结论
ANFIS 兼具神经网络与模糊逻辑的优点,适合处理非线性及不确定性问题。自提出以来,在自动控制、信号处理等领域都得到广泛应用。借助 Python 的 anfis 库,可轻松实现 ANFIS 模型并将其应用于各种场景。