Genetic Algorithm

Introduction to Genetic Algorithm (GA)

Genetic Algorithm (GA) is a computational model inspired by biological evolution, natural selection, and the inheritance of successful traits. It simulates life processes through code and belongs to the family of evolutionary computation methods. Its core ideas are rooted in Darwin’s theory of evolution. While a deep understanding of genetics is not required to use genetic algorithms, grasping their basic principles helps us better understand and apply them.

In this introduction, we will first review some key concepts from genetics and biological evolution to lay the foundation for understanding the code simulation in genetic algorithms. Then, we will outline the basic workflow and essential components of genetic algorithms.

Darwinian Evolution and Genetic Algorithms

Genetic algorithms can be seen as a simplified implementation of Darwinian evolution in nature. The core principles of Darwinian evolution can be summarized as follows:

• Variation/Mutation: The traits (also called characteristics or attributes) of individual members within a population may differ, resulting in a certain degree of diversity among individuals.
• Heredity: Some traits can be inherited from parents to offspring, causing the offspring to resemble their parent individuals to some extent.
• Selection: In a given environment, populations usually compete for limited resources. Individuals that are better adapted to the environment have a competitive advantage, making them more likely to survive and produce more offspring.

In short, the evolutionary process maintains diversity among individuals in a population. Individuals that are better adapted to their environment are more likely to survive, reproduce, and pass on their advantageous traits to the next generation. As generations progress, the species as a whole becomes better adapted to its environment.

Key mechanisms driving evolution include:

• Crossover: Also known as recombination, it produces offspring by combining the traits of two parents. Crossover helps maintain diversity in the population and gradually brings together better traits over time.
• Mutation: Refers to random changes in traits. Mutation introduces stochastic changes and plays a crucial role in evolution.

Genetic algorithms draw inspiration from these ideas, aiming to find the optimal or near-optimal solution to a given problem. In Darwinian evolution, what is preserved are the traits of individuals in the population; in genetic algorithms, what is preserved is a set of candidate solutions to a given problem, also known as individuals. These candidate solutions undergo iterative evaluation and are used to create the next generation of solutions. Typically, better solutions (with higher fitness) have a greater chance of being selected and passing their “traits” (parts of the encoded solution) to the next generation of candidate solutions. In this way, as generations are updated, the set of candidate solutions becomes better at solving the current problem.

Core Concepts of Genetic Algorithms

Understanding genetic algorithms requires mastering the following core concepts:

• Genotype: In nature, processes such as reproduction, inheritance, and mutation are characterized by the genotype, which is a collection of genes that make up a chromosome. In genetic algorithms, each “individual” (candidate solution) consists of a “chromosome” representing its set of genes. For example, a chromosome can be represented as a binary string, where each bit represents a gene.
• Population: Throughout the execution of a genetic algorithm, a collection of multiple individuals is maintained, known as the population. Since each individual is represented by a chromosome, the population can be viewed as a set of chromosomes.
• Fitness Function: In each iteration of the algorithm, the fitness function is used to evaluate the quality of each individual in the population. The objective function is the mathematical expression of the problem that the genetic algorithm aims to optimize or solve. Individuals with higher fitness scores represent better solutions and are more likely to be selected for reproduction, passing their traits to the next generation. As the genetic algorithm progresses, the quality of solutions typically improves and fitness increases. Once a solution with a satisfactory fitness value is found, the genetic algorithm can be terminated.
• Selection: After calculating the fitness of each individual in the population, the selection process determines which individuals will be used for reproduction and to produce the next generation, based on their fitness values. Typically, individuals with higher fitness values are more likely to be selected and pass their genetic material to the next generation. However, to maintain population diversity, individuals with lower fitness still have a certain probability of being selected, so their genetic material is not completely discarded.
• Crossover: To create new individuals (offspring), the crossover operation exchanges segments of chromosomes between two selected parent individuals from the current generation. This produces two new chromosomes representing their offspring.
• Mutation: The purpose of mutation is to periodically and randomly alter the genes of individuals in the population, introducing new patterns into the chromosomes and encouraging the algorithm to search unexplored areas of the solution space. Mutation can manifest as random changes in genes, such as flipping a bit (changing 0 to 1 or 1 to 0) in a chromosome represented by a binary string.

Basic Process of Genetic Algorithm

Genetic algorithms typically follow these basic steps:

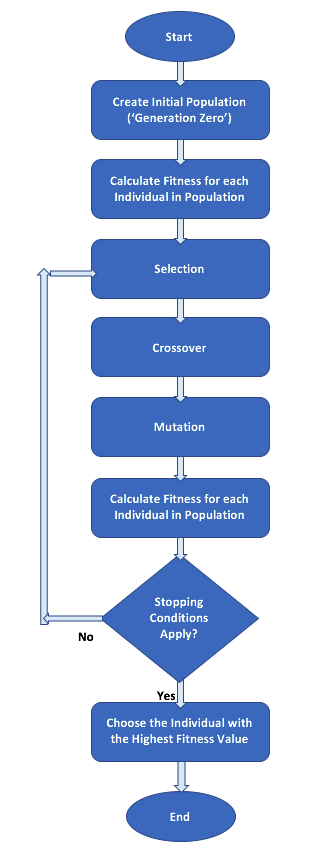Basic Flow of Genetic Algorithm

1. Initialization The initial population is a set of randomly generated valid candidate solutions (individuals) for the current problem. Since genetic algorithms use chromosomes to represent each individual, the initial population is essentially a collection of chromosomes.

2. Fitness Calculation/Evaluation For each individual in the population, calculate its fitness value using a predefined fitness function. This operation is performed once for the initial population. In subsequent generations, fitness must be recalculated for new individuals produced through selection, crossover, and mutation genetic operators. Since fitness calculation for each individual is typically independent of other individuals, this process has potential for parallel computation. Note that the selection phase usually favors individuals with higher fitness scores. Therefore, genetic algorithms inherently search towards maximizing fitness scores. If the actual problem requires finding a minimum value, the original objective function values need to be transformed during fitness calculation, such as multiplying by -1 or taking the reciprocal (while handling potential division by zero issues).

3. Applying Genetic Operators: Selection, Crossover, and Mutation Apply the three core genetic operators - selection, crossover, and mutation - to the current population in a specific order and probability to produce a new generation. The new generation typically inherits characteristics from superior individuals in the current generation.
   • Selection: This operation selects advantageous individuals from the current population for the mating pool, preparing them for reproduction.
   • Crossover: This operation creates offspring from selected parent individuals. This is typically done by exchanging parts of chromosomes between two selected parent individuals to create two new chromosomes representing their offspring.
   • Mutation: This operation randomly makes small changes to one or more chromosome values (genes) of newly created (offspring) individuals. Mutation probability is usually set very low to avoid disrupting learned good patterns while introducing new genetic diversity.
4. Termination Condition Various conditions can be checked to determine if the algorithm should stop. Two most common stopping conditions are:
   • Maximum Number of Generations: This is a common limitation used to control algorithm runtime and computational resource consumption.
   • Convergence: This occurs when the best individual’s fitness hasn’t improved significantly over several generations. This can be implemented by recording the best fitness value obtained in each generation and comparing the current best value with the best value obtained a predetermined number of generations ago. If their difference is less than a preset threshold, the algorithm can be considered converged and stopped.

After completing these steps, if the termination condition is not met, the new population replaces the old one, and the process repeats from step 2 (fitness calculation). This iterative process continues until the termination condition is satisfied. The algorithm ultimately outputs the individual with the highest fitness found so far as the optimal or near-optimal solution to the problem.

Hyperparameters of Genetic Algorithms

The performance of genetic algorithms is significantly influenced by various parameter settings (hyperparameters). The evolution process can be optimized by adjusting these hyperparameters and the specific implementation of genetic operators. Here are some common hyperparameters and their functions:

• Population Size: Represents the number of individuals in each generation of evolutionary simulation. Population size is typically related to the complexity of chromosomes (such as the length of gene sequences). For individuals with more complex gene sequences, a larger population might be needed to evolve individuals with high fitness.
• Number of Generations: Similar to epochs in deep learning, this represents the number of iterations in the genetic algorithm’s evolution. In genetic algorithms, each generation involves evolving the entire population. The appropriate number of generations is usually determined by the length and complexity of chromosomes, as well as the difficulty of the problem. The number of generations can be balanced with population size - for example, using a larger population with fewer generations, or vice versa.
• Crossover Rate: Indicates the proportion of individuals in each generation that undergo crossover operations, or parameters used to determine the position or number of crossover points. A higher crossover rate means more individuals will participate in recombination, which helps explore new regions of the solution space but may also disrupt existing good patterns.
• Mutation Rate: Represents the probability of mutation for each gene in an individual. Higher mutation rates typically lead to more variations in the population, which may be beneficial for solving complex or multi-modal optimization problems and helping the algorithm escape local optima. However, excessive mutation rates can hinder convergence towards optimal solutions and make the search process unstable. Conversely, lower mutation rates produce fewer population variations and may cause premature convergence to local optima.

Genetic algorithms laid the foundation for broader Evolutionary Computation (EC) methods. Fundamentally, the concepts of evolution and “survival of the fittest” are key components of all evolutionary computation methods.